平均絶対誤差は、そのシンプルな定義と直感的なビジネス関連性により、モデルを評価する際に実務家にとって最初の選択肢となります。対照的に、評価指標であるRanked Probability Score は、一見するとそれほど魅力的な関数ではありません。その抑止力となる名前は、扱いにくい正式な定義によく合致しており、サプライ チェーンの実務者はほとんど誰もそれを知らず、ましてや使用していないことを示しています。しかし、彼らは見逃しています!順位付け確率スコアは、平均絶対誤差を確率予測の領域、つまり自身の不確実性を「知っている」予測に自然に拡張したものです。直感的な解釈が可能で、平均絶対誤差の深刻な問題のいくつかを解決します。順位付け確率スコアは、平均絶対誤差よりもさらにビジネスを反映し、統計的不確実性を考慮しているため、象牙の塔の統計理論と日常の実践を調和させることができます。
妥当なビジネス標準:平均絶対誤差
「需要予測モデルを評価するにはどの指標を使用すればよいでしょうか?」
この質問に対する答えは、通常「平均絶対誤差」であり、かなり確固とした根拠に基づいています。絶対誤差 (AE) は、多くの場合、予測が「外れた」ことによるコストを適切に反映します。イチゴが 8 かご売れると予測して 8 かご分在庫したが、実際の需要が 9 だった場合、AE は 1 となり、不満を持った顧客 1 人が競合他社に目を向けます。同じ需要 9 個に対して予測が 11 個のバスケットの場合、AE は 2 であり、処分するイチゴが 2 バスケットあります。観測された結果 9 の場合、AE は予測の関数として次のグラフの青い線で表示されます。
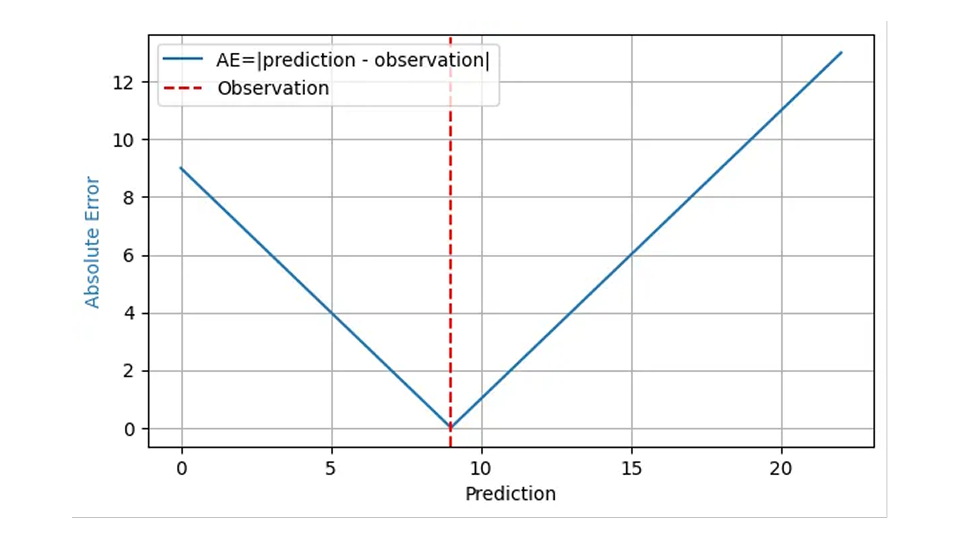
予測誤差の財務的影響は通常、予測誤差自体に比例するため、多くの予測と結果にわたる AE の平均である平均絶対誤差 (MAE) は、少なくとも 1 個の過剰在庫が 1 個の不足在庫と同じ財務的影響を与えるという仮定の下では、ビジネス コストを反映します。平均二乗誤差 (MSE) では、誤差が大きいほど「1 つずれる」ことでコストが増大すると評価されますが、これはビジネスではまったく非現実的です。平均絶対パーセント誤差 (MAPE)、つまり正規化された AE の平均 (平均 (AE/観測結果)) には、予期せぬ重大な落とし穴があるため (この以前のブログ投稿で説明されているように)、需要予測では安全に無視できます。
したがって、実践者は、モデルを評価するための最初の簡単な選択肢として、MAE またはその正規化された変形である相対 MAE、RMAE = MAE / 平均 (結果) を使用することを強くお勧めします。ただし、MAE と RMAE の標準値は規模に依存します。牛乳瓶 (売れ筋) の予測では、一部の特殊電池 (売れ行きの悪い商品) の予測よりも MAE が大きく、RMAE が低くなるのは当然です。確かに、それを見るのは簡単ではありません。そのため、その問題に特化したブログ投稿は 1 つの投稿に収まらず、 「Forecasting few is different」パート 1とパート 2に分割されました。
MAE はシンプルでよく知られており、関連性が高いので、代替案についてブログ記事を書いたり読んだりする必要があるでしょうか?確かに、評価基準を盲目的に信頼することは、データに関して最も非科学的な行為の 1 つです。MAE を徹底的に調べて、本当に期待どおりに動作するかどうか、またそうでない場合はどのように修正するかを確認しましょう。長い話を短くすると、AE を評価するときに予期しない厄介な複雑な問題に遭遇しますが、これらは、関連性はあるものの非常に過小評価されている指標であるRanked Probability Scoreによって穏やかに解決されます。
待ってください、そんなに急がなくても!確率予測における平均絶対誤差の評価方法
これまで、「予測」は、予測対象そのもの(販売された商品の数、つまりイチゴのバスケット、リンゴ、牛乳のボトル、赤い T シャツの数)と同様に、単なる数字であると仮定してきました。そのような予測 (数値) と実際の観測 (別の数値) の差を計算することは、まったく問題ではありません。リンゴが 10 個売れると予測し、実際に売れたのは 7 個で、AE は 3 です。統計学の博士号は必要ありません。
しかし、微妙な点があります。リンゴが 10 個売れるのではなく、10.4 個売れると予測していたらどうなるでしょうか。在庫を手元に置いておくという私の決断は、どのようなものだったでしょうか?おそらく私は依然としてリンゴを 10 個注文していたでしょう。つまり、予測の 0.4 という小さな差は業務上の違いを生まず、ビジネス結果は同じだったでしょう。それでも、絶対誤差は 3 ではなく 3.4 と、わずかに大きくなります。最初の図の予測における絶対誤差の滑らかな動作は誤解を招きます。予測と実際の差は、ビジネスに関連する数量ではなく、注文されたアイテムの数と実際の差です。整数しか発生しないとわかっているのに、なぜ整数以外のものを予測するのでしょうか?
この食い違いの理由 (非整数値を予測するが、測定するのは整数量のみ) は、ほとんどの予測が、ターゲットに対する普遍的で評価に依存しない「最良推定値」を表す「ポイント予測」ではなく、確率分布を提供するものであるためです (心配ありません。統計学の博士号はまだ必要ありません)。これらは、それぞれの起こりうる結果がどの程度起こりうるかを示します。10.4 を予測する場合、顧客がリンゴを 1 個に切って 0.4 個買うとは想定しませんが、起こりうる結果「11」、「12」、「13」は 10.0 を予測する場合よりも起こりうると見なします。したがって、予測は目標と比較できる単なる数値ではなく、関数です。この議論はどの分布にも当てはまりますが、このブログ投稿全体を通して、予測される確率分布はポアソン分布であると仮定します (関連するブログ投稿については、こちらとこちらを参照してください)。
ここで、1.3、3.8、または 11.7 を予測するときに暗黙的に主張する確率分布を確認してください。
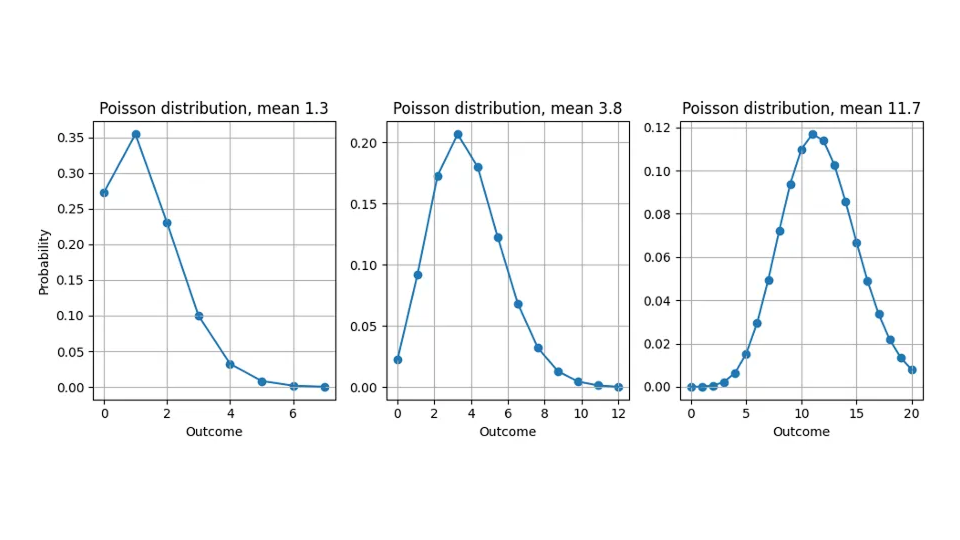
絶対誤差の評価に戻ります。数値から関数を減算するにはどうすればよいでしょうか?確率分布から販売された商品 7 個を減算しても意味がありません。比較を可能にするには、予測される確率分布を 1 つの数値で要約する必要があります。この要約数値はポイント推定値と呼ばれ、観測された実際の値から差し引くことで誤差を算出することができます。
確率分布はさまざまな方法で要約できます。平均値が最も直接的ですが、分布は、最も可能性の高い結果 (モード)、確率分布を 2 つの等しい半分に分割する結果 (中央値)、またはその他の処方箋によって要約することもできます。
さまざまなポイント推定値の中には、他のものよりも自然に感じるものもあります。最も気に入った要約を選択するだけでよいのでしょうか?いいえ、正しいポイント推定値は選択された評価基準によって決定されます。言い換えると、どのエラー メトリックを使用して予測を評価するか (MAE、MAPE、MSE など) を選択できますが、その評価の予測を要約する方法は私が選択します。MAE で優勝するためのポイント推定値は、MAPE はもちろん、MSE で優勝するためのポイント推定値とも異なります。この選択は恣意的、あるいは不誠実に聞こえるかもしれませんが、これは確率予測の計り知れない表現力を反映しています。確率予測には、単なる単一の「最善の推測」よりもはるかに多くの情報が含まれています。評価方法、つまりエラー メトリックによって「最良」が実際にどのように定義されているかに応じて、特定の評価方法で優先される値がそれに応じて選択されます。言い換えれば、「最善の予測を教えてください」という質問は、「最善」がどのように定義されているかが明確でない限り意味がありません。単一の確率予測では、予測の評価方法に応じて、さまざまなポイント推定値、つまり「最善の推測」が生成されます。
二乗誤差 (SE) の場合、点推定値は分布の平均になります。絶対パーセント誤差 (APE) の場合、点推定値は非常に直感に反する機能であり、ここでは取り上げませんが、 MAPE 評価で予期しないパラドックスが発生します。
絶対誤差には平均ではなく分布の中央値が必要であり、確かにそれは重要である。
AE (絶対誤差) の場合、正しい点推定値は中央値になります。はい、平均値ではなく中央値です。また、平均値だけを使用することはできません。AE にとって中央値のみが最適である理由を説明します。1 つの予測、つまり 1 つの分布を取り、それを平均 3.8、中央値 4 のポアソン分布とします。この予測が与えられた場合、いくつのアイテムを買いだめしますか?結果は必ず整数になるので、3.8 にはなりません。適切な在庫量を見つけるには、その分布からの結果を観察するときに平均的に見つかる AE が可能な限り小さくなるように推定値を選択しましょう。
私たちは、この分布全体を単一の数値、つまり運用上最適な在庫量に凝縮する適切なポイント推定値を探します。この図では、3つの異なる推定値(3、4、5)を試しています。
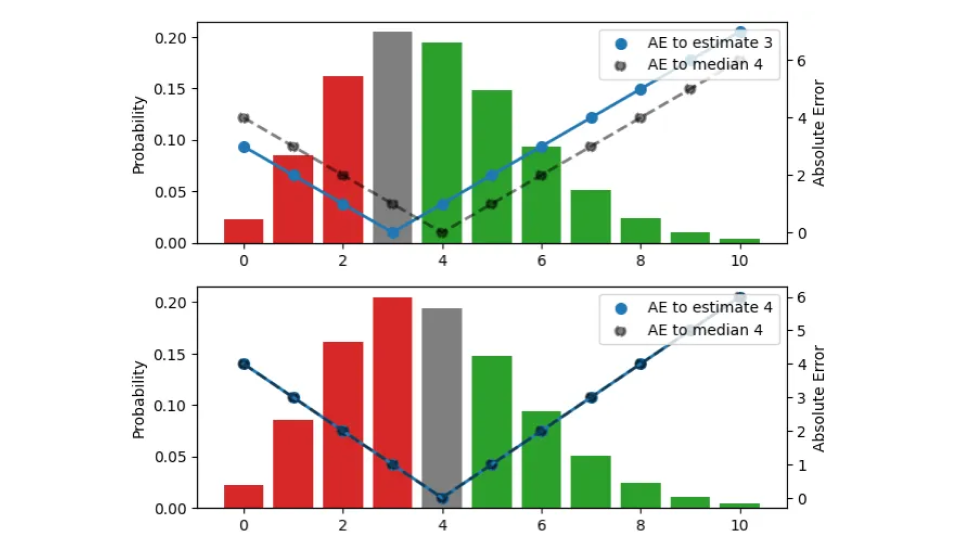

バー(左のスケール)で視覚化された確率分布は、3 つのパネルで同じです。上のパネルでは推定値 3 が視覚化され、真ん中のパネルでは推定値 4 が視覚化され、下のパネルでは推定値 5 が視覚化されています。推定値と結果の間の AE は青い点で示され、実線で結ばれています (右のスケール)。中央値 4 に関する AE は黒い点で示され、破線で結ばれています。たとえば、推定値が 3 (上のパネル) の場合、結果 3 の誤差は消え、青い実線は 0 になります。観測値が 4 または 2 の場合、誤差は 1 になります。
バーの色は、予測された結果が推定値より小さい (赤) か大きい (緑) かによって絶対誤差に寄与するかどうかを示し、バーの高さはそれが発生する確率です。結果が推定値と一致する場合、エラーへの寄与はゼロとなり、灰色で表示されます。推定値を 1 単位上にシフトすると、パネルが 1 つ下に移動し、赤いバーの下と灰色のバーの下のすべての観測値が、シフトされた新しい推定値の 1 単位以上の誤差の原因となります。以前の推定値 3 では、結果 2 に誤差 1 がありましたが、推定値 4 では、同じ結果に誤差 2 があります。一方、シフト後、緑のバーがあったすべての観測値は、誤差が 1 単位少なくなります。推定値 3 では、結果 5 に誤差 2 がありましたが、推定値 4 では、誤差が 1 に減少します。
推定値が 1 単位増加した場合に何が起こるかをまとめてみましょう。分布における AE の期待値は、推定値以下の結果については増加し (実際よりもさらに過大に予測する)、推定値より大きい結果については減少します (実際よりも過小に予測する)。増加は赤と灰色のバーの合計面積に比例し、減少は緑のバーの面積に比例します。
完全に類推すると、推定値を 1 単位減らすと、緑色のバーの下または灰色のバーの下の観測値はそれぞれ 1 単位の誤差の増加に寄与し、赤色のバー内のすべての観測値は 1 単位の誤差の減少に寄与します。
特定の分布では、推定値を 1 つ上下にシフトすると、結果として得られる絶対誤差の予測値が増加または減少し、最小値を探すことで適切な点推定値を検索できます。あなたはすでに次のような経験則を考案しているかもしれません: 現在の見積もりで、ほとんどの結果が予測を下回る場合は見積もりを減らし、ほとんどの結果が予測を上回る場合は見積もりを増やします。予測超過と予測不足に関連する確率質量の差(「赤」バーと「緑」バーの合計面積の差)が灰色のバーよりも小さい場合にのみ、誤差をそれ以上改善することはできません。中央のパネルがこれに該当します。推定値は、その下と上の確率質量がほぼ一致するような値になっており、どちらの方向に動いても総誤差が増加します。この推定値は中央値と一致します。確率分布が与えられた場合、絶対誤差を最小化する点推定値は、ケースの半分で結果よりも高くなるか低くなります。
この点は、しばしば考慮されないため、強調する価値があると思います。分布の平均の最良の推定値が 7.3 である場合、たとえば 9 という観測値に対する絶対誤差を評価する正しい方法は、9 から 7.3 を引くのではなく、その分布の中央値 (ポアソン分布の場合は 7) を 9 から引くことです。操作上、7 は、予測値が 7.3 である場合に買いだめするアイテムの数と正確に一致します。驚くべきことに、予測が 7.1 か 7.3 かは関係なく、株式決定の平均値を正確に見積もるのに役立ちません。整数を決定する必要があります。ただし、計画のためにより高いレベルで予測を集計する場合は、7.1 と 7.3 の区別が重要になります。
平均値と中央値のこの区別は、些細なことのように思えるかもしれません。結局のところ、確率を 2 つの等しい半分に分割する値とその分布の平均は非常に似ているように見え、ほとんどの有益な分布 (小売業に関係するポアソン分布など) では近い値になります。ただし、2 つの分布の平均は同じでも、中央値が異なる場合があります。また、他の 2 つの分布は、中央値が一致するが、平均が異なる場合があります。平均値と中央値を同義語として使用するだけでは、最適な予測を実際に見つけることはできません。
平均絶対誤差の予期せぬ欠点
確率予測の絶対誤差を評価する方法がわかりました。分布を点推定値の中央値(在庫する商品の数)で要約し、観測された結果からその中央値を差し引いて絶対値を取得します。これを次の図で視覚化してみました。
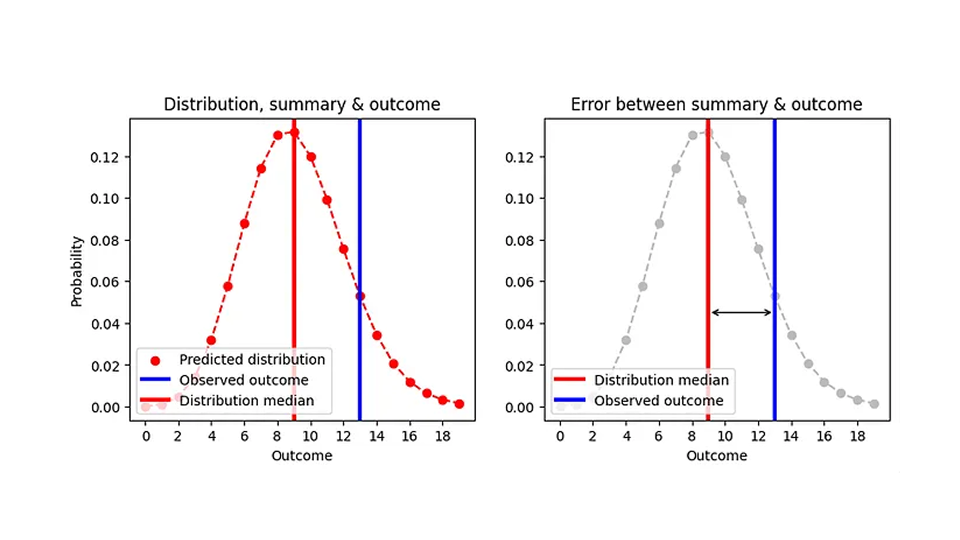
中央値は常に整数であるため、2 つのまったく異なる分布で同じ絶対誤差が生じる可能性があります。たとえば、次の図に示すように、予測が明らかに異なるにもかかわらず、ポアソン予測 8.7 (中央値 = 9) とポアソン予測 9.6 (中央値 = 9) の AE は同じです。
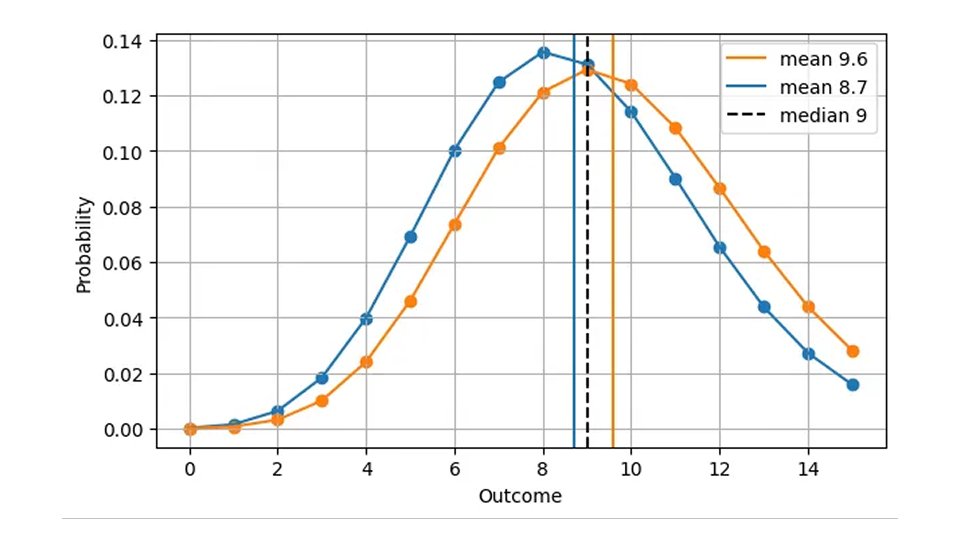
これは運用上は理にかなっています。どちらの場合も、特定の日に 9 個のアイテムを在庫しておくのが適切です。したがって、最初の図のより現実的なバージョンである予測の関数としての AE は次のようになります。
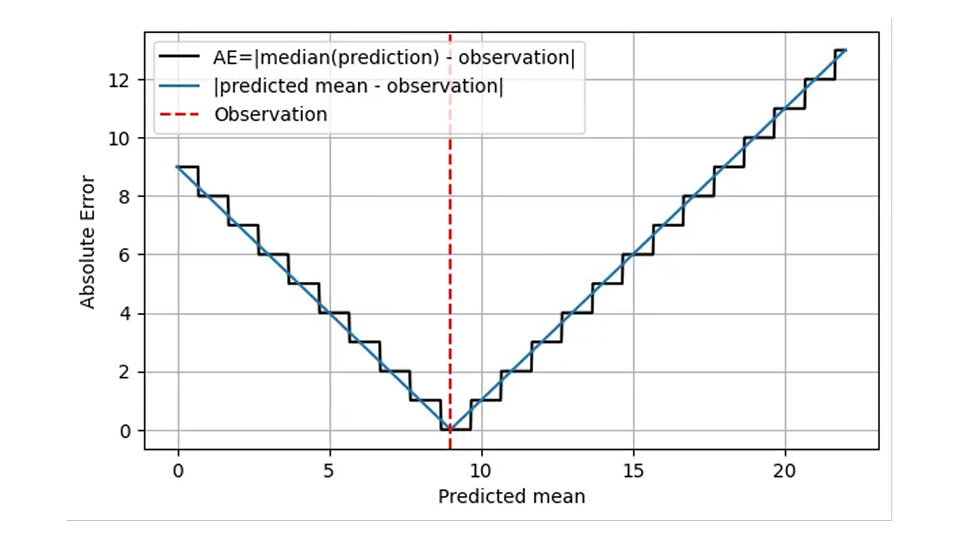
AE は予測の中央値 (黒線) を使用して計算され、整数値のみを想定します。x 軸の意味をもう少し具体的に説明します。これは単なる「予測」ではなく、予測された平均です。
この階段形状は、AE が粗粒度で不正確であることを示しています。つまり、平均 8.7 と 9.6 の分布は目で見れば区別できますが、AE では区別できないのです。MAE だけでは、ゆっくりと変化する項目に対して非常に大きな影響を与える特定のしきい値を超える予測の精度の向上には役立ちません。1.7 と 2.6 の相対的な差は 53% ですが、1.7 の予測の AE と 2.6 の予測の AE は同じです。この粗粒度の挙動には厄介なジャンプ、つまり分布の中央値がある整数値から次の整数値にジャンプする値での不連続性が伴います。運用上、特定の日、場所、品目について 1.7 と予測しても 2.6 と予測しても違いはありません。適切な在庫量は 2 です。ただし、予測は計画のためにより高い集約レベルでも使用されます。このような高いレベルでは、1.7 と 2.6 の違いがはっきりとわかります。次の 100 日間、サプライヤーに 170 個注文するか 260 個注文するかによって大きな違いが生じます。
予測平均値が予測期間あたり約 0.69 未満の場合 (売れ行きの悪い商品)、絶対誤差が最も良くなる予測は 0 です。非常に劇的なことに、予測値が 0.6、0.06、0.006 のいずれの場合も、桁が 2 桁異なるにもかかわらず、絶対誤差は同じです。予測 0 は、サプライ チェーンではまったく役に立ちません。完全な 0 予測の悪循環に陥るからです。つまり、在庫 0 個、販売 0 個、そして前回の予測 0 が自己実現的に正しいということになります。













