パート 1 では、予測平均と観測結果の差をとるだけで平均絶対誤差を評価する通常の方法に挑戦しました。絶対誤差の操作的解釈に従って、分布を単一の数値で要約するには、正しい点推定値である中央値を使用する必要があることがわかりました。しかし、これは MAE のかなり好ましくない特性を伴います。MAE は粒度が粗く、不連続であり、動きの遅いものには役に立ちません。
ランク付けされた確率スコアのステージをクリアする
明らかに、このブログ投稿の最初の部分で私が示した状況は満足できるものではありません。MAE は不連続かつ不正確であり、予測平均値が 0.69 未満の動きの遅い銘柄に対しては役に立たないのです。それでも、コストはエラーに比例するという合理的なビジネス解釈は、依然として魅力的です。修正できますか?
中央値を削除して、より適切な平均値などの他の要約を使用することはできませんか?残念ながら、中央値と平均値の区別が無関係であるかのように装っても、それが事実になるわけではありません。その方法では問題は解決されず、むしろ新たな問題が生じます。つまり、MAE が誤って評価された場合に勝つ予測は偏ったものになります。
要約として中央値に結び付けられている場合、AE を改善する可能性は何でしょうか?変更できる点が 1 つあります。それは、「要約する」と「エラーを計算する」という 2 つのプロセスの順序です。現在、最初に要約(分布を点推定値にマッピング)し、次に誤差(「点推定値 - 結果」)を計算します。深呼吸して、下のグラフ (左側) に示すように、2 つのステップを入れ替えてみましょう。予測される分布 (赤) と 1 つの観測結果 (青) が与えられた場合、予測される結果ごとに AE を計算してみましょう (黒い矢印)。
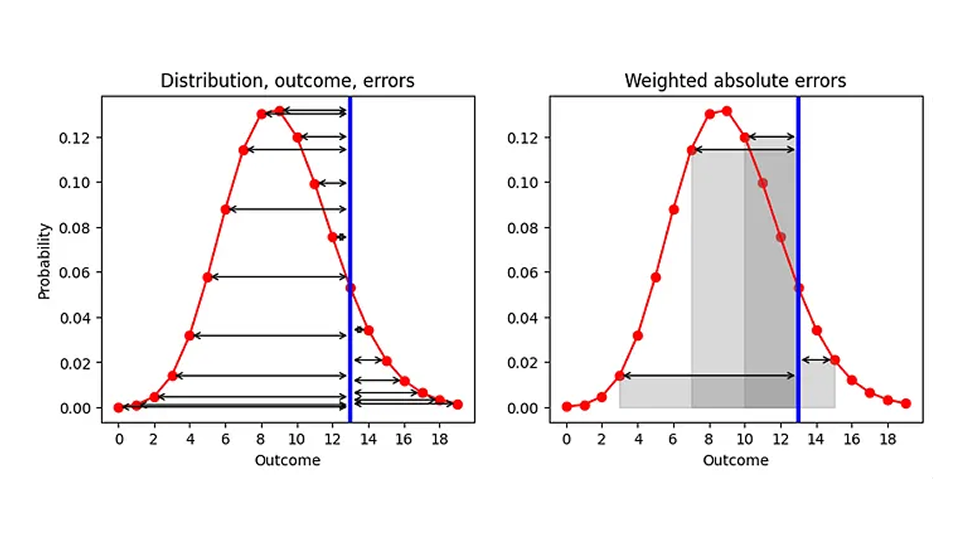
結果は、各結果に対して 1 つずつの AE のリストです (実際の結果と一致する予測 (AE は 0) も含みます)。私たちの目標は AE を 1 つの数字に置き換えることなので、それらの多数の AE を要約する必要があります。AE の平均をとり、その平均における重みとして各結果に割り当てた確率をとります。幾何学的には、右のグラフのいくつかの結果に示されているように、誤差矢印と x 軸で囲まれた領域を合計しています。
この規定は、数値と確率分布の間の距離の合理的な定義です。つまり、起こり得る結果までの各距離を、その結果に割り当てられた確率で重み付けするのです。エッジケースとして、分布が 1 つの結果(この結果が確実に実現されると予測する決定論的予測)を除いてどこでも 0 である場合、従来の AE、つまりその決定論的に予測された結果と観測値の間の距離の絶対値を回復します。弊社の改良された AE は、決定論的予測のための従来の AE になります。
処方箋は次の式で表すことができます。
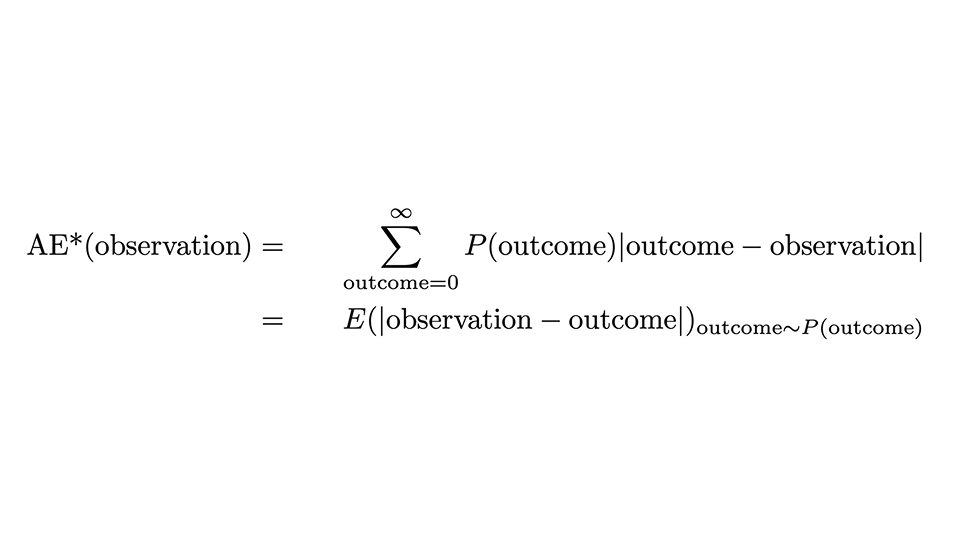
少し恐ろしく見えますが、簡単に見ていきましょう。観測値に対する AE*、つまり「補正された AE」は、その単一の観測値に対する AE ですが、予測確率 P(結果) を重みとして、すべての可能性のある結果にわたって平均化されます (結果の合計)。2 行目は、結果が確率分布に従って分布する場合、これが観測と結果の間の絶対距離の期待値と一致することを表しています。
すごい乗り心地!まだそこまでには至っていませんが、ほぼ到達しています。AE* は正確には Ranked Probability Score ではなく、その扱いにくい名前の由来もまだわかりません。
上記で定義された AE* には、望ましくない特性が 1 つあります。真の分布が特定の平均値を持つポアソン分布である場合、その平均値と一致したときに最低かつ最良の AE* が達成されるのではなく、わずかに小さい平均値で達成されます。あなたの予測が AE* で勝った場合、それはおそらく偏っていて、予測が低すぎます。その理由は、分布の絶対的な幅が平均値とともに増加し、より小さな平均値が有利になるためです (ここでも、以前のブログ投稿 [Forecasting Few is Different 1&2 へのリンク] を宣伝する機会があります)。この問題は解決可能です。それを考慮するには、分布の予想幅の半分、つまり予測分布から取得した 2 つのランダムな結果間の予想距離を減算する必要があります。最後に、ランク付けされた確率スコアが得られます。
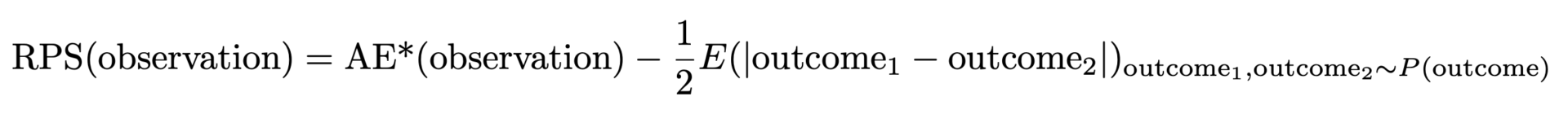
しかし、なぜこれは Ranked Probability Score (RPS) と呼ばれ、それほど人気がないのでしょうか?RPS は通常、多くの確率、ステップ関数、累積確率を含む抽象的な数式を通じて導入されます。多くの場合、純粋に確率論的な解釈で提示されますが、これは確率論や統計学に詳しい人にとっては納得のいくものですが、実践者にとっては理解しにくいものです。2 つの定式化 (私たちの「改良された AE」と確率論的な定式化) が一致するというのは実に注目すべきことです。つまり、(実践者の目には) 醜いアヒルの子が美しい白鳥に変わるのです。
順位付け確率スコアが平均絶対誤差の欠点をどう解決するか
この投稿の最初の部分で、MAE には不都合な特性がある、つまり粒度が粗く、不連続で、動きの遅いものには役に立たない、と主張しました。「改良型 MAE」である RPS はこれらの問題を解決するのでしょうか?確かにそうです!
次のグラフでは、RPS (黒線) と AE (青線) を比較しています (この場合も、観測値は 9 (赤の破線))。結果 9 から大きく離れた予測の場合、RPS と AE は同様に動作し、RPS は AE をわずかに下回ります。予測された平均値と観測値が 9 で一致すると、AE はゼロになりますが、RPS は少し懐疑的です。RPS は分布を認識しているため、予測された分布の中央値と結果がぴったり一致することも偶然である可能性があると判断します。おそらく、その日の実際の販売率は 7 で、観測された需要が 9 だったのは少し運が良かっただけです。したがって、RPS が 0 になることはありません。個々の結果は、確率的予測が正しかったことを明確に証明するものではありません。結果 9 から離れる場合、AE は厳格であり、対応するコストで「外れること」を直ちにペナルティします。RPS はここではより寛容であり、AE ほど急速には増加しません。これは、「少しずれている」ことは不運による可能性があり、すぐに制裁する必要がないことを反映しています。これはビジネスの現実に非常によく一致しています。業務は、多くの場合、わずかな逸脱が許容されるような形で計画されます。誰もが決定論的な予測を望んではいるものの、真剣に期待している人はいません。そのため、安全在庫が存在します。偏差が大きくなると、実際のコストが発生し始めます。
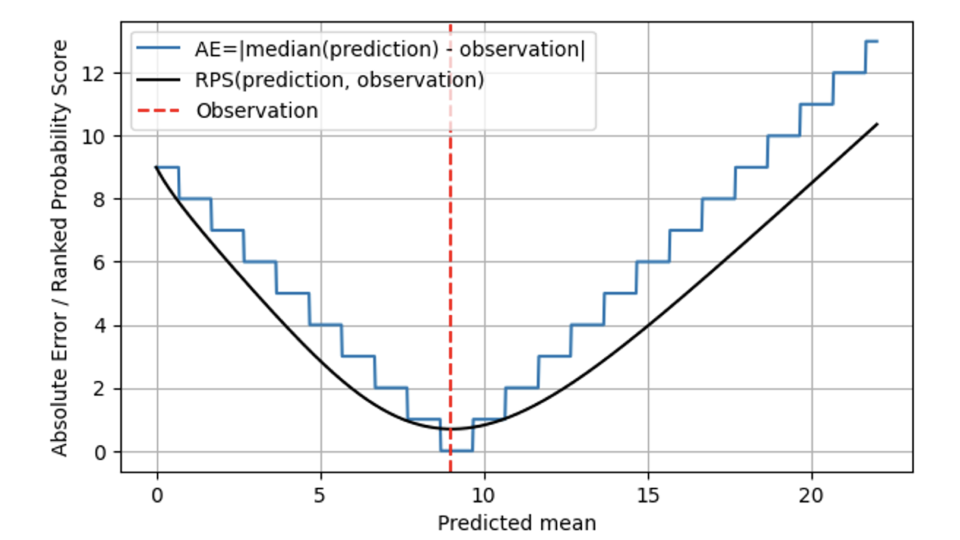
全体的に、ランク付けされた確率スコアは異なる値の間を「ジャンプ」しませんが、数学的に言えば、予測される平均値は連続しています。AE の場合、予測値 8.7、9.3、9.6 は区別できませんが、RPS の場合は区別できます。RPS の最小値は、予測平均値 9 でちょうど達します。
売れ行きの遅い商品の場合、RPS は役立ちますが、魔法の薬ではありません。RPS を使用しても、100 日に 1 回売れる商品と 200 日に 1 回売れる商品を区別することは依然として困難です。ただし、RPS は、0.6、0.06、0.006 などのわずかに異なる予測値でも異なる値を想定します。
RPS は MAE の多くの問題の解決に役立ちますが、RPS でも解決できない課題が 1 つあります。それは、販売の遅い顧客と速い顧客の動作を異なるものにしてしまう避けられないスケーリングです。ただし、メトリックをスケーリング対応にする方法 (このブログで部分的に説明されています [Forecasting Few is different 1&2 へのリンク]) は、AE に適用されたのと同じ方法で RPS に適用できます。相対 MAE と比較すると、相対平均 RPS (平均 RPS を平均観測値で割ったもの) はこのプロットでより滑らかな形になり、両方のメトリックで達成可能な最良の値を示しています。
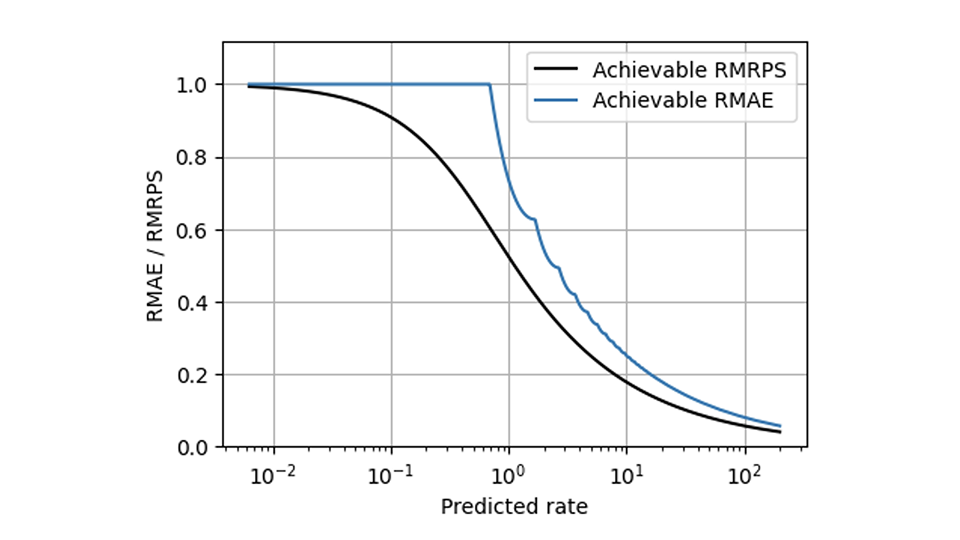
MAE の代わりに MRPS を使用する必要があるのはどのような場合ですか?
意味のある予測は決して決定論的かつ確実なものではなく、確率的かつ不確実なものであり、評価ではこれを考慮する必要があります。人間は不確実性を好まないと言うのは控えめな表現です。人間は不確実性を嫌うのです。人々は完全な確実性を得るために、期待効用をかなり犠牲にする覚悟がある(リスクが致命的である場合、そうするのは合理的なことだ)。ビジネス関係者は、予測は「あくまでも」確率的な予測を提供するものだと言われると、代わりに決定論的な予測を望むことが多く、予測者はそのような予測の作成を拒否することで関係者を失望させる必要があります。しかし、避けられない不確実性を明確にすることは弱さの表れではなく、信頼性の表れです。
考えられるすべての結果の確率を含む確率分布の表現力全体を 1 つの数字に凝縮することは、見た目どおり単純化され、粒度が粗く、乱暴です。ただし、これはアイテムを在庫するときに操作上実行する必要があることです。したがって、概念的な観点から見ると、ランク付けされた確率スコアは、「結果は予測からどの程度離れているか」という質問に対して、絶対誤差よりもはるかに優れた答えを提供します。
予測の確率的性質が重要でない場合は、AE と RPS の差は無視でき、AE と RPS は互換的に使用できます (前者は後者よりも計算が簡単であり、後者はわずかに小さい値を想定しています)。つまり、確率分布の幅が、発生する典型的な誤差よりもはるかに小さい場合、予測者である私は、発生する誤差を「どうしようもない避けられないノイズ」のせいにすることができません。たとえば、ある商品の販売数が 1,000 倍になると予測し、特に野心的ではなく、結果が 800 ~ 1,200 倍程度であれば満足できる場合、RPS と AE の違いはわずかになります。簡単にするために、AE を使用するべきです。
中程度からゆっくりとした動きの領域、つまり 0.8、7.2、16.8 などの平均値を予測する場合は、分布を 1 つの数値に凝縮して AE を評価するか、RPS を使用してもう少し複雑なパスをたどるかによって違いが生じます。「1」を予測する場合、つまり「1」が観測される確率はわずか約37%であり、0が観測される確率も同様に約37%であることを意味します。したがって、中程度から低調な販売体制において予測の確率的な性質を無視することは危険であり、誤解を招く可能性があります。しかし、これで確率分布を説明する方法がわかりました。ランク付けされた確率スコアを使用することで、統計学者と実務家の両方を満足させる予測評価の野生生物の中の美しい白鳥として見られるようになることを願っています。













