後知恵選択バイアスは、販売頻度全体にわたって予測精度を評価する際に、確率予測の予測値と観測された実績値が適切にグループ化されていない場合に発生します。一方、後知恵選択バイアスは、特定の確率予測のバイアスに関して誤った結論に導く狡猾な罠であり、最悪の場合、より良いモデルよりも悪いモデルを選択してしまうことになります。一方、その解決と説明は、サンプルの代表性、確率予測、条件付き確率、平均への回帰、ベイズの定理などの統計的基礎に触れています。さらに、予測から私たちが直感的に何を期待するか、そしてそれが必ずしも合理的ではない理由について考えるきっかけにもなります。
予報は個別のカテゴリーに関係することがあります - 明日は雷雨があるでしょうか?— あるいは連続量— 明日の最高気温は何度になるでしょうか?ここではハイブリッド ケース、つまり離散量(たとえば、ある日に販売される T シャツの数) に焦点を当てます。このような販売数は離散的であり、0、1、2、13、または 56 になる可能性がありますが、-8.5 や 3.4 になることは絶対にありません。私たちの予測は確率的なものであり、T シャツが何枚売れるかを正確に知っているふりをしないでください。現実的だが野心的に狭い(つまり正確な確率分布はポアソン分布です。したがって、当社の予測によって、実際の販売プロセスを推進すると考えられるポアソン率が生成されるものと想定します。
かなり平凡な予測ですか?
予測が発行され、実際の売上が収集され、次のような表を通じて予測が評価されたと仮定します。
| 観察された販売頻度 | 平均観測売上高 | 平均予測 |
| 遅い 0、1、2個/日 | 0.804 | 1.373 |
| 中くらい 1日3~10個 | 5.119 | 4.601 |
| 速い 1日10個以上 | 13.880 | 11.041 |
データは、観測された販売頻度によってグループ化されます。つまり、すべての日を、T シャツがたまたま少数 (0、1、または 2 回)、中程度 (3 ~ 10 回)、または多数 (10 回以上) 販売されたグループに分けます。一見すると、この表は「売れ行きの遅い商品は過剰に予測され、売れ行きの速い商品は過少に予測されている」と明確に主張しているように見えます。この予測には明らかに大きな欠陥があるので、私たちはすぐにそれを修正しようとするでしょうか、そうしないでしょうか?
実際のところ、おそらく驚くべきことに、すべては順調です。はい、確かに売れ行きの遅い商品は過剰に予測され、売れ行きの早い商品は不足して予測されていますが、予測は予想どおりに機能します。「平均観測売上高」の列と「平均予測」の列は同じになるはずだという私たちの予想に欠陥があります。私たちは、悪い予測ではなく、心理的な問題、つまり非現実的な期待に対処しているのです。確率予測では、結果の可能性のある各グループについて、平均予測が平均結果と一致することは決して約束されておらず、また実現されることもありません。
なぜそうなるのか、この難問を満足のいく形で解決するにはどうすればよいのか、そして同様の偏見を避けるにはどうすればよいのかを検討してみましょう。
私たちは実際何を求めているのでしょうか?
少し立ち止まって、表が何を表しているかを言葉で表現してみましょう。データは、実際に観測された売上を使用してバケット化されます。つまり、予測と観測が特定の範囲(売れ行きの悪い商品、中程度の商品、売れ行きの速い商品)にあるかどうかをフィルタリング(条件付け)します。最初の行には、T シャツが 0 回、1 回、または 2 回販売されたすべての日が含まれ、中央の列には次の情報が表示されます。

つまり、2、1、または 0 であるすべての観測値をグループ化したバケット内の観測値の平均です。これは間違いなく 0 から 2 の間の数値であり、0.804 になります。右側の列には、同じ観測値のバケットに対する期待平均予測が含まれています。

つまり、2 以下のすべての観測値について、対応する予測を取得し、これらすべての予測の平均を計算します。
先験的には、最初の式と 2 番目の式が同じ値を取る理由はありませんが、直感的にはそうなることを望みます。平均予測が平均観測と等しくなることを期待するのは、それほど要求しすぎではないようですね。
| 観察された販売頻度 | 平均観測売上高 | 平均予測 |
| 遅い 0、1、2個/日 | E (観測値 | 観測値 ≤ 2) | E (予測 | 観測 ≤ 2) |
| 中くらい 1日3~10個 | E (観測 | 観測 ≤ 3, ≤ 10 ) | E (予測 | 観測 ≤ 3, ≤ 10] ) |
| 速い 1日10個以上 | E (観察 | 観察 ≥ 11) | E (予測 | 観測 ≥ 11]) |
将来を見据えた予測と過去を振り返る事後判断
語源の通り、予測は将来を見据えたものであり、将来の結果を観察する確率を提供します。
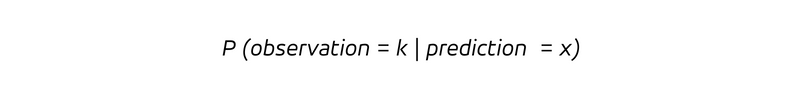
これは、予測率が x である場合に、結果 k を観測する条件付き確率です。条件付き確率があるため、予測値が x であると仮定して観測値の確率分布を考慮します。偏りのない予測の場合、予測 x を条件とする観測の期待値、つまり予測値が x であるという仮定の下での平均観測値は次のようになります。
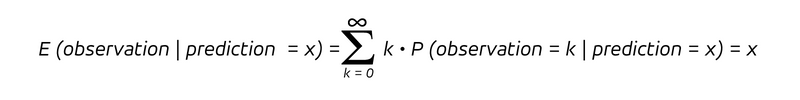
これが、あらゆる偏りのない予測が約束することです。つまり、同じ値 x のすべての予測をグループ化すると、結果として得られる観測値の平均は、まさにこの値 x に近づくはずです。分布はさまざまな形をとることができますが、このプロパティは重要です。
表をもう一度見てみましょう。左の列では、予測によるグループ化/条件付けではなく、結果によるグループ化/条件付けを行っています。したがって、右側の列では、将来を見据えた「予測 x を前提とした場合、平均的な結果はどうなるか」という質問ではなく、過去を振り返る「特定の結果 k を前提とした場合、平均的な予測は何だったか」という質問になります。
過去を振り返る記述を将来を振り返る記述で表現するために、ベイズの定理を適用する。

過去を振り返る質問と将来を振り返る質問は異なり、その答えも異なります。予測と結果の無条件確率を表す P (予測 = x ) と P (観測 = k ) という他の用語も登場します。したがって、特定の結果が与えられた場合の平均予測の期待値は次のようになります。

ミニマルな例
E (予測 | 観測 = m) はどのような値をとるでしょうか?なぜ観測値 m に単純化しないのでしょうか?
ほとんどの場合、 E (予測 | 観測 = m) ≠ m となります。理由を見てみましょう!
販売率 5 のポアソン分布に従い、毎日同じように売れる T シャツを考えてみましょう。まったく同じ予測レート 5 が毎日適用されます。しかし、結果はさまざまです。明らかに、5 は結果 4 以下の場合には過大評価であり、結果 6 以上の場合は過小評価です。結果別に再度グループ化すると、次のようになります。
| 観察された販売頻度 | 平均観測売上高 | 平均予測 |
| 遅い 1日5個未満 | 3.0082 | 5 |
| 中くらい 1日5個 | 5 | 5 |
| 速い 1日5個以上 | 7.2844 | 5 |
もう一度、この表から、売れ行きの悪い日は過剰に予測され、売れ行きの良い日は過少に予測されたと結論付けることができます。そして実際その通りでした。予測は常に 5 なので、すべての観測値E (予測 | 観測値 = m) = 5が成り立ちます。
予測は依然として「完璧」です。結果はまさに予測どおりに動作し、レート 5 のポアソン分布に従います。予測が下回ったり上回ったりする印象は、純粋にデータの選択の結果です。5 を超える結果を選択すると、予測より 5 上だが予測が下回った結果が保持され、5 を下回る結果を選択すると、予測より 5 下だが予測が上回ったイベントが保持されます。確率予測では、一部の結果が過小に予測され、一部の結果が過大に予測されることは避けられません。予測が偏りのないものと期待することで、特定の予測 m に対して予測不足と予測過剰が均衡すると期待されます。私たちが期待できないのは、過剰予測または過少予測された観測を積極的に選択したときに、これらがそれぞれ過剰予測または過少予測されないということです。
現実的な状況では、毎日まったく同じ値を想定する予測を扱うことはなく、予測自体は変化します。それでも、「かなり大きい」または「かなり小さい」結果を選択することは、予測が不足または過剰だったイベントをバケット内に保持することになります。したがって、一般にE (予測 | 観測 = m) ≠ mとなります。より正確には、m が非常に大きく、それを選択すると予測が不足しているイベントを選択することになる場合は、 E (予測 | 観測 = m) < mとなります。m が十分に小さく、それを選択すると予測が過剰であるイベントを選択することになる場合は、 E (予測 | 観測 = m) > m となります。
決定論的な予測 — 常に知っておくべきでした!
なぜこれが私たちにとって不可解なのでしょうか?平均観測値と平均予測値の間の矛盾になぜ私たちは不快感を覚えるのでしょうか?私たちの直感は、決定論的予測の特徴である予測と観察の平等性にかかっています。確率の言語では、決定論的予測は次のように表現されます: P (観測 = 予測) = 1およびP (観測 ≠ 予測) = 0
予測者は、観測結果が予測と完全に一致すると信じています。つまり、予測値と観測値は確率 1 (または 100%) で一致しますが、その他の結果はあり得ないと考えられます。それは自信に満ちた、大胆な発言だと言うこともできる。条件付き確率で表現すると、次のように要約できます。

言葉で言えば、k 個を販売すると予測するたびに (縦棒の後の条件)、k 個を販売することになります。決定論は、k を予測するたびに k を観測することを意味するだけでなく、すべての観測 k が事前に k であると正しく予測されることも意味するため、次の式が成り立ちます。
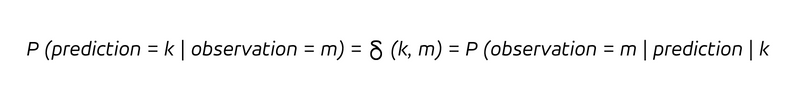
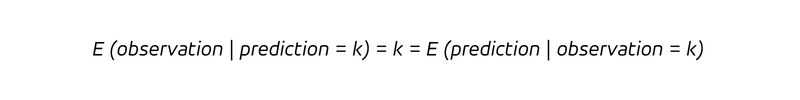
決定論により、過去を振り返る質問と未来を振り返る質問の区別は時代遅れになります。決定論的な予測では、結果を観察することで何か新しいことを学ぶことはなく (すでにわかっていたことです!)、信念を更新することもありません (すでに正しかったのです)。
出現するすべての確率分布が、唯一可能な結果で 100% のピークにまで崩壊するような決定論的予測の場合、事後判断による選択バイアスは発生しません。つまり、常に、あらゆる状況において、私たちは事前に正確に知っていた、したがって知っているべきだったと仮定するのです。測定値がそれ以外のことを示している場合、「決定論的」予測は間違っています。
あらゆる真剣な予測は確率的である
確率予測は決定論的予測よりも弱い主張をします。確率予測の場合、各結果 m が平均して m になると予測されるという考えを放棄する必要があります。そのため、決定論的予測は非常に魅力的に見えます。しかし、毎日の T シャツの売上を決定論的に予測することは現実的でしょうか?あなたがそうすることができて、明日の T シャツの売上が 5 であると予測できたと仮定しましょう。つまり、何が起こっても(事故、病気、雷雨、突然の心変わりなど)、明日赤い T シャツを買うであろう 5 人の名前を挙げることができるということです。どうすればそのような確実性のレベルに到達できると期待できるのでしょうか?あなたは次の日に赤い T シャツを買うと確信したことがありますか?たとえ 5 人の友人が、どんな状況でも明日 T シャツを 1 枚買うと約束したとしても、他のすべての潜在的顧客の中で、他の誰かが T シャツを買う可能性をどうやって排除できるでしょうか。特定の非常に特異なエッジケース(顧客が非常に少ない、在庫レベルが実際の需要よりはるかに少ない)を除けば、商品の正確な販売数を決定論的に予測することは不可能です。不確実性はある程度までしか抑えることができず、現実的な予測はすべて確率的なものになります。
評価衛生
表 1 を反駁する別の方法があります。表を設定することで、予測に偏りがあるかどうか、またどの方向に偏りがあるかという統計的な質問をします (統計的有意性の質問は今のところ無視し、表示されるすべてのシグナルが統計的に有意であると仮定します)。他の統計分析と同様に、予測分析にも偏りが生じる可能性があります。結果によって選択した方法は、選択バイアスの典型的な例です。「売れ行きの遅いもの」、「中程度のもの」、「売れ行きの速いもの」のグループ内のイベントは、予測と観察のセット全体を代表するものではなく、予測が低かったものと予測が高かったものに分類されました。また、予測評価では「将来の情報」と呼ばれるものを使用しました。予測と観測をグループ化するバケットは、予測の時点ではまだ定義されていませんが、事後的に確立されます。したがって、私たちが行ったように表を設定することは、統計分析の基本原則に違反しています。
平均回帰
私たちが今遭遇した現象、つまり極端な出来事が実際に起こったほど極端になるとは予測されていなかったという現象は、「平均への回帰」に直接関係しています。これは予測さえ必要のない統計的現象です。季節性やその他の時間依存パターンを示さない製品の売上の時系列を観察しているとします。ある日に観測された売上高が平均売上高よりも大きい場合、翌日の観測値は今日のものより小さくなることはほぼ確実であり、その逆も同様です。繰り返しになりますが、非常に大きい値または非常に小さい値を選択すると、プロセスの確率的な性質により、正または負のランダムな変動が選択される可能性が高くなり、売上は最終的に「平均に回帰」します。心理学的には、私たちは平均値への回帰(純粋に統計的な現象)を何らかの積極的な介入のせいにする傾向があります。
解決策: 結果ではなく予測でグループ化します。選択バイアスに対して警戒を怠らないでください。
この難問から抜け出す方法は何でしょうか?結果ごとにグループ化することで、予測に関して「かなり大きい」または「かなり小さい」値を選択することになります。つまり、代表的なサンプルではなく、偏ったサンプルを取得することになります。この選択バイアスにより、当然ながらそれぞれ「かなり予測不足」または「かなり予測過剰」な結果が含まれるバケットが生成されます。平均予測と平均観察が「低速」、「中速」、「高速」の動きの項目内で同じであるはずだと信じている場合、後知恵選択バイアスに陥ることになります。私たちは、この 2 つの列の間の矛盾を受け入れ、受け入れて生きなければなりません。幸いなことに、ベイズの定理を使用して現実的な期待値を得ることができます。したがって、1 つの解決策は、テーブル内の別の列であり、その列にはバケットごとの平均予測の理論的期待値が含まれており、そのバケット内の実際の平均予測と比較することができます。つまり、後知恵選択バイアスを定量化し、理論的に再現し、集計されたデータが理論的な期待と一致するかどうかを確認することができます。
しかし、もっと簡単な解決策は、データに対して別の質問、つまり予測が約束するものと一致する質問をすることです。これにより、これらの約束が果たされているかどうかを直接確認できます。結果バケットごとにグループ化する代わりに、予測バケット、つまり予測される売れ行きの遅い商品、中程度の売れ行きの商品、売れ行きの速い商品ごとにグループ化します。ここで、予測の約束(特定の予測を与えられた平均売上高がその予測と一致する)が満たされているかどうかを確認できます。この例では、次の表が得られます。
| 予測販売頻度 | 平均観測売上高 | 平均予測 |
| 遅い 1日3個未満 | 1.288 | 1.267 |
| 中くらい 1日3個 | 5.247 | 5.229 |
| 速い 1日3個以上 | 12.855 | 12.950 |
測定の総数を考慮すると、統計的有意性のテストは否定的、つまり、観測された平均売上高と平均予測の間に有意差がないことを示します。私たちの予測は、世界的に偏りがないだけでなく、予測層ごとにも偏りがないと結論付けます。
一般に、予測時に既知の情報に基づいてフィルタリングすることで予測を評価でき、予測はすべてのテストで偏りのないものでなければなりません。ただし、フィルターには、観測時に発生するランダムな変動などの将来の情報を含めることはできません。このような将来の情報は、予測時点の将来についてのみ自然が決定します。
ここまで到達したら、何を持ち帰るべきでしょうか?(1)結果で選択する場合、代表的なサンプルが得られません。(2)自分の期待に対して懐疑的になる。直感的に非常に合理的に思える期待でも、実は間違っていることが判明する。(3)期待を明確にし、よく理解されている事例に対してそれをテストする。













