小売予測において、関心のある数量は特定の製品に対する顧客の需要、たとえばイチゴのバスケットがいくつ要求されているかなどです。実際には、登録された売上高という、わずかだが重要な異なる数量が観察されます。売上は需要を反映しますが、キャパシティ、つまり在庫レベルによって制約されます。つまり、バスケットの需要が 20 個あるのに在庫が 12 個しかない場合、販売されるのは 12 個だけで、購入を希望していた 8 人の顧客の要望は満たされません。売上と需要の違いは些細なことのように思えるかもしれませんが、このブログ記事では、売上と需要を取り違えると偏ったトレーニングや欠陥のあるモデル評価につながる理由を説明します。有限在庫が売上にどのような影響を与えるか、また有限在庫が関係する実際の状況に自信を持って対処するために最も重要な落とし穴を回避する方法を学びます。
需要と売上
あなたが思いつく最も正確な予測、つまりどんな賭けでもできる常に正しい需要予測とは何でしょうか?多くの場合、答えは「常に「0」を予測するだけです」です。需要予測がゼロの場合、商品は 1 つも注文されず、棚には商品がなく、販売される商品もありません。ゼロ予測はまさにその通りで、観測されたゼロ売上と完全に一致しました。この絶対的に正確な予測は、明らかに、あなたのマネージャーを満足させる予測ではありません。
この極端な例は、何を求めるかについて注意する必要があることを示しています。小売業者の目標は、正確な予測を作成することではなく、持続可能なビジネスを運営することです。このパラドックスは、需要予測における根本的なジレンマも明らかにしています。つまり、予測自体が最終的に提供される在庫のレベルに影響を及ぼし、その評価を危うくするのです。この影響は正当な理由で存在し、予測はそのために行われたと主張するかもしれません。しかし、在庫レベルによって販売できる商品の数に上限が設定され、観測できる販売値が人為的に制限されます。これにより、仮想需要(「どれだけの量が求められているか」)と観測された売上(「どれだけ販売されたか」)の間に矛盾が生じます。観測された売上は、どちらが低いかに応じて、実際の需要または入手可能な在庫となります。
このブログ投稿では、需要と売上の問題を厳密に確率的に扱う以外に方法はないことを納得していただけると思います。需要と売上の区別、これらの数量の細心の取り扱い、そして正確に予測し観察するものが、モデルのトレーニングと評価を成功させ、正しく行うための鍵となります。
物事を具体的に(そしておいしく)するために、新鮮なイチゴの入ったバスケットを販売する小売業者を考えてみましょう。販売されたバスケットの整数値の数は、「個」として扱うことができます。残念なことに、これらの超新鮮な食料品は、日中に売れないと廃棄されてしまいます。したがって、過剰発注、つまり要求されているよりも多くの在庫を持つことはコストがかかるため、避けるべきです。一方、イチゴを買おうと思って、近所のスーパーで探したらすでに売り切れだったと想像してください。あなたは、支払う意思が満たされず、イライラした顧客になります。したがって、注文不足、つまり要求された量よりも少ない在庫を抱えることは、顧客満足度と収益および利益の損失の両面でコストがかかります。
小売業者は、廃棄と売上損失を慎重に相殺するために、適切な数のイチゴバスケットを注文する必要があります。もちろん、この発注問題を解決するには、販売されるバスケットの数ではなく、要求されるバスケットの数を正確に予測する正確な需要予測が必要です (上記の自己達成的「0」予言を思い出してください)。
いくら売れるでしょうか?
需要予測についてもう少し詳しく調べて、その意味を分析してみましょう。需要予測により、要求されるアイテムの数がわかります。しかし、「9.7 個のバスケットが要求されます」とは具体的にどういう意味でしょうか?明らかに、イチゴのかごを端数だけ売ることはできないので、文字通りの解釈はばかげています。それでも、私たちは予測を受け入れて直感的に理解し、それを、販売されるバスケットの平均予想数、つまり同じ状況が何度も繰り返された場合に平均して販売されるバスケットの数(そして、在庫は常に十分であると仮定します)に関する主張として解釈します。したがって、私たちの予測では平均予想売上高のみが示されるため、何らかの確率分布、つまり 1、2、3、… のバスケットが売れる可能性についての概念が暗黙的に隠されています。それらの確率がどの程度であるか、または個々の観測値 (つまり、実際の販売数) が平均 9.7 にどの程度近いかは省略されています。
確率分布が隠れているカーペットを持ち上げて、どのように見えるかを確認してみましょう。以下の表を使用して例を説明します。事前に、期待値が 9.7 である確率分布は、非常に異なる形を取る可能性があります。左側のパネルに示すように、0 に遭遇する確率が 51.5%、20 に遭遇する確率が 48.5% であると考えてください。この結果、平均値は 9.7 になります。9 や 10 など、9.7 に近い値は観測されず、0 や 20 などの極値のみが観測されます。中央のパネルの確率分布では、10 に 70% の確率、9 に 30% の確率が割り当てられています。期待値も 9.7 ですが、確率の塊は平均値に近い値に集中しているため、典型的な販売数の適切な推定値となります。平均が 9.7 である分布の集合は無限に大きく、それらの分布のほとんどは不正な動作をします (数学者が好んで言うように「病的な」)。幸いなことに、右側のパネルのポアソン分布のような、単純で正常な確率分布を想定できます (なぜそれが合理的な選択なのかを知るには、ブログ記事「少数の予測は異なる」をお読みください)。
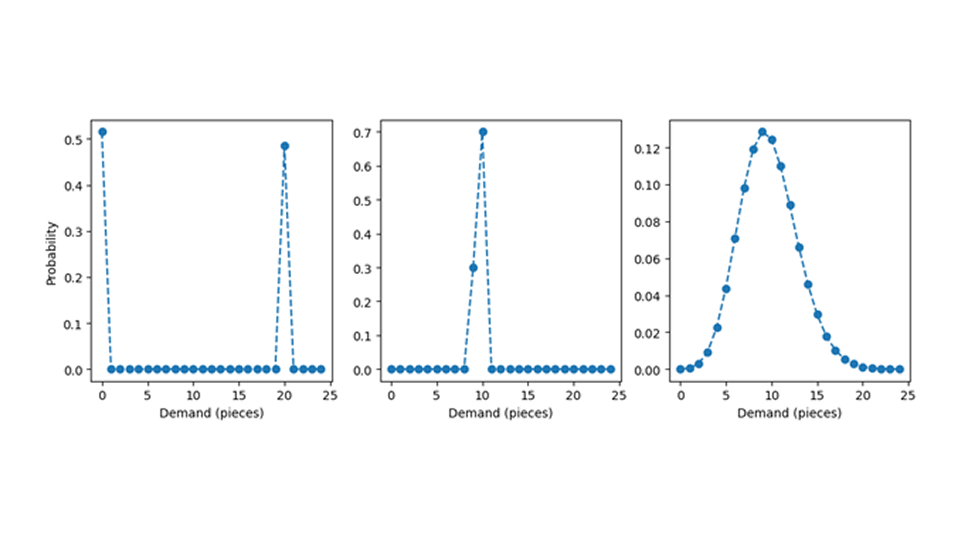
このテキスト全体を通じて、予測によって予測されるポアソン分布の平均が生成され、需要は実際にポアソン分布に従う、つまり予測が正しいと仮定します。この理想的なシナリオでも、ブログ投稿を正当化するほど多くの複雑な要素が存在します。
有限株式がどのように情報を検閲するか
有限の容量をゲームに迎え入れましょう。需要分布が与えられれば、それぞれの可能な需要値を結果として得られる売上値にマッピングすることによって、売上分布が得られます。利用可能な在庫数と等しいかそれ以下の需要値の場合、需要はそのまま 1:1 で売上に変換されます。つまり、利用可能なバスケットが 12 個ある場合、要求されたバスケットが 5 個であれば 5 個が販売され、要求されたバスケットが 12 個であれば 12 個が販売されます。需要が在庫より大きい場合、つまり、容量が十分でない場合は、販売はその在庫値によって制限されます。13 個、25 個、または 463 個のバスケットが要求されている場合、販売されるのは 12 個だけです。すべての在庫が売り切れた場合、これを「キャパシティヒット」イベントと呼びます。しかし、13、25、または 463 バスケットの需要に関連する確率質量は「どこかに行く」必要があり、実質的には総株式数が要求される確率に追加されます。平均需要 9.7 と異なる容量 (16、12、8) の販売確率分布を次の図に示します。
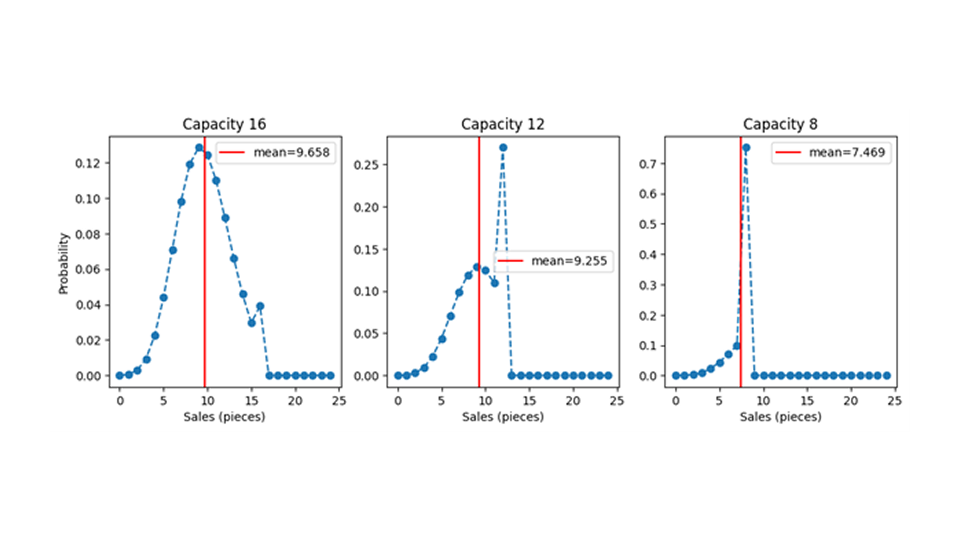
有限のキャパシティーは、情報を取り除く方法で需要を検閲します。つまり、キャパシティーを 16 に設定し、キャパシティーヒット、つまり 16 件の販売が観察された場合、需要が少なくとも16 であったと推測することしかできず、需要が 16 であったか、25 であったか、または 7,624 であったかはわかりません。実際の需要には、あなたにはわからない値(たとえば 47)がありますが、観察されるのは 16 だけです。容量には限りがあるため、私たちは本当に取り返しのつかない形で情報を失っています(顧客満足度だけではありません)。この情報の損失により、限られた容量内でモデルをトレーニングしたり評価したりすることが難しくなります。
プロットには、予想される平均売上高も垂直の赤い線で表示されます。驚くべきことに、容量が予想される需要よりも大きい場合でも、有限の容量は売上の期待値に影響を与えます。つまり、需要が 9.7 と予測され、在庫が 12 個ある場合、平均して 9.7 個未満しか販売されないことになります。予測どおりに販売するには、平均して予測よりも多く在庫しておく必要があります。これは混乱を招くかもしれません。個々のイベントの場合、売上は需要と在庫の最小値にすぎません。しかし、販売確率分布の平均は、確率分布の形状を考慮する必要があるため、必ずしも予想需要と容量の最小値になるわけではありません。この驚くべき動作の理由は、平均予測需要の値が、平均的には相殺される平均値周辺の変動に依存しているためです。つまり、マイナスの変動 (販売されるアイテム数が 9.7 より少ない場合もあります) がプラスの変動 (販売されるアイテム数が 9.7 より多い場合もあります) によってバランスが取られます。容量が有限である場合、必要な正の変動は抑制され、正の変動と負の変動の打ち消しは発生しなくなります。これにより、容量が平均予想需要よりも大きい場合でも、平均予想売上高は低い値になります。
以下のグラフは、予想需要が 9.7 の場合の、予想売上を容量の関数として示しています。容量が予想される需要よりもはるかに大きい場合(たとえば、約 20)、有限の容量によって影響を受けるイベントはまれになります。その結果、予想販売数は影響を受けず、9.7 に近くなります。容量が 5 のように小さい場合、その容量に達することはほぼ避けられず、平均するとその容量に近い値が販売されます。7 から 14 あたりで移行が起こり、容量は売上に強い影響を与えますが、完全に決定的な影響を与えるわけではありません。
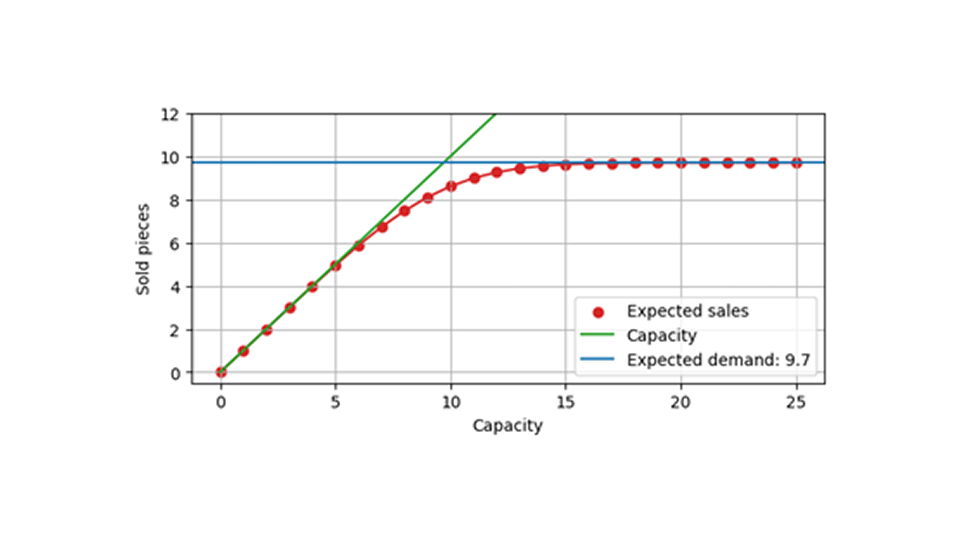
検閲された需要に基づくモデルのトレーニングと評価
これで、私たちの主力である売上の確率分布、つまりキャパシティ検閲済み需要分布を制御できるようになりました。次は、そのような状況でモデルをトレーニングおよび評価するときに注意する必要があることを理解しましょう。
異なる体制を区別する必要があります。キャパシティが毎日限界に達した場合、実際の需要は決してわからず、需要の下限値(「5 個を販売したので、需要は少なくとも5 個でした」)しかわかりません。幸いなことに、これは非現実的なシナリオです。毎日キャパシティが限界に達すると、多くの不満を持った顧客と満たされない需要に対処しなければならず、そのような運営形態を長く維持できる小売業者は存在しません。供給制限によってそうせざるを得なくなった場合、価格を引き上げることで需要を誘導することを検討するかもしれない。
反対に、容量がまったく満たされない場合は、データ サイエンスを実行するための最適な環境が整います。つまり、実際の需要を毎日読み取り、容量に関する議論を基本的にすべて無視することができます。しかし、データ サイエンティストの夢は、サステナビリティ担当者にとっては悪夢です。このような発注戦略の結果、膨大な量の無駄が生じることになります。予想需要が 9.7 である場合、在庫切れが 1,000 日間に 1 回だけ発生するようにするには、21 個の在庫を保持する必要があります。
したがって、需要が供給能力に達する場合(一日のある時点で商品が売り切れる)もあれば、達しない場合(夕方には在庫が残る)という状況に遭遇するのが一般的です。これは合理的です。なぜなら、無駄を避けることと在庫切れを避けるという相反する目標の間の妥協が望ましいからです。
最善のモデルを構築することと、最善のビジネスを運営することは矛盾することを認識すべきです。持続可能なビジネス戦略(廃棄物が完全に「無料」ではないが、少なくともある程度は回避されている場合)では、商品が在庫切れになることは避けられません。しかし、最高のデータ サイエンスは、在庫切れが絶対に発生しないことが保証され、すべての販売値が需要を直接反映しているときに行われます。私たちはビジネス環境でデータサイエンスに取り組んでいるため、中間的なシナリオや時折発生する在庫切れに耐えなければなりません。













