すべてを同じように扱う — 一般的には良いように聞こえるが、確率予測評価ではそうではない 前回の食料品の例に戻り、リンゴ、ツナ缶、瓶について話しましょう。ここで、APE を比較することは、2 つの理由からあまり意味がありません。
定義上、売れ行きの悪い商品は売れ行きの速い商品よりも売れる頻度は低くなります。したがって、信頼性の低い売れ行きの悪い商品の予測がビジネスに与える影響は、同様に信頼性の低い売れ行きの良い商品の予測がビジネスに与える影響よりもはるかに小さくなります。売れ筋商品の在庫切れによる 5% の売上損失は、販売業者にとっては単に不都合なだけですが、ベストセラー商品の 5% の売上損失は非常に深刻なものになり得ます。結局のところ、ビジネスでは絶対数が重要になります。主力製品の米国における総需要を 20% も過大に予測しているのですか?おそらく、問題があり、大量の売れ残り在庫を処理する必要があり、それがビジネス全体を危険にさらす可能性もあります。ツバルにおける同じ製品の総需要を20%も過大に予測しているのですか?ツバルに対して何も悪い気はしませんが(本当に、悪気はありません!)、その間違いであなたのビジネスが破綻することはないと思うので、おそらく安心してください。主力商品カテゴリーに比べ、小規模な品揃えや市場では、はるかに大きな相対誤差を許容できます。なぜ、限界商品や顧客グループを、本当に大きな魚と同じぐらい重要視するのでしょうか?
この明らかな違い (小さいものは小さい、大きいものは大きい) に加えて、微妙に見えますが重要な統計的効果があります。それは、達成可能な予測精度のスケール依存性です。1 日に 10 回販売される製品の場合、完璧な予測であっても 10% オフになることは避けられないことがあります (ポアソン不確実性がある場合)。1 日に 10,000 回売れる製品を 10% オフにすることは、明らかに問題があることを示しています。ビジネス上、売れ行きの遅い商品は売れ行きの速い商品ほど重要ではないだけでなく、当然相対的な誤差も大きくなります。この点については、以前のブログ記事「少数の予測は異なる パート 1 」および「パート 2」で詳しく説明しています。
上記の食料品予測については、おそらくその日のマグロに関しては運が悪かっただけでしょう。追加の水のボトル 16 本については、あまり言い訳できないようです。したがって、絶対パーセンテージ誤差 (APE) では、ビジネス用語 (不等なものを均等に重み付けする) でも統計用語 (達成可能な値には予測値自体のコンテキストが必要) でも、達成可能な予測の品質をうまく捉えることができません。
MAPEによる補充管理は在庫レベルを壊滅的に高める 言い換えれば、MAPE は予測の質そのものを示す良い指標ではありません。3 つの異なる状況で 20%、70%、90% に達したかどうかは、すぐに解釈できる意味を持ちません。特定の MAPE 値が与えられた場合、結論を急ぐべきではありません。しかし、MAPE 値自体は全体的なモデルの品質についてほとんど何も教えてくれないとしても、特定の予測状況では、MAPE で勝った予測が最良の予測であるはずだと予想できます。私が今から説明するように、その弱い期待も捨て去る必要があります。
四半期に 1 回程度しか売れない低迷商品から、1 日に 100 回も売れる急速商品まで、さまざまな商品を扱うスーパーマーケットを考えてみましょう。アイテムの補充は、毎日の MAPE 最適予測を選択し、それに従って事前注文するシステムによって行われます。つまり、MAPE が最も低くなる予測値を選択します。そのスーパーマーケットの業績はどうでしょうか?
簡単にするために、リンゴ、バナナ、カシューナッツ、ドラゴンフルーツ、ナスの 5 つの代表的な製品に注目します。これらの製品の真の平均 1 日の販売率はそれぞれ 0.01、0.1、1、10、100 です。最も遅いリンゴは四半期に 1 回程度しか売れず、最も速いナスは 1 日に 100 回売れます (これらの数字は現実世界の妥当性のためではなく、数学的な明瞭さと単純さのために作られたものだとお考えなら、その通りです)。この思考実験では、これらの販売率がわかっており、それらは各製品の構成ごとに可能な限り最良の予測です。ポアソン分布を使用すると、何が起こるかをシミュレートでき、最適な MAPE での予測値はいくらになるかをシミュレートできます。
各製品について、次の表は、真の販売率 (偏りのない最良の毎日の予測)、シミュレートされた MAPE、最適化された MAPE 勝利予測、シミュレートされた MAPE、および結果として生じるバイアスを示しています。
製品 真の日次販売率、偏りのない日次予測 真の販売率のMAPE MAPE受賞の毎日の天気予報 MAPE受賞予測のMAPE MAPE受賞予測の予測バイアス リンゴ 0.01 99% 1 0.25% +9,900% バナナ 0.1 90% 1 2.5% +900% カシューナッツ 1 23.3% 1 23.3% 0% ドラゴンフルーツ 10 31% 9 29% -10% ナス 100 8.11% 99 8.05% -1%
実際の 1 日の販売率は、構造上、予想売上高の平均値であるため、補充システムへの入力としては間違いなく最適なものであることを覚えておいてください。補充で代わりに MAPE 勝利予測を使用するとどうなりますか?スーパーマーケットでは売れ行きの悪い商品を過剰に在庫しています。毎日、リンゴ 1 個、バナナ 1 個、カシューナッツ 1 個が補充されますが、リンゴは 100 日に 1 回、バナナは 10 日に 1 回しか売れません。リンゴやバナナは山積みになり、カシューナッツは順調ですが、ドラゴンフルーツの需要は満たされていません。平均して、ドラゴンフルーツを購入したいと思っていた顧客 1 人が、買い物を完了せずに店を出て行きます。動きの速いナスの場合、1% の誤差は許容できるかもしれませんが、実際の販売率が 1 に等しくない限り、「最良」の予測が常に偏っていることは驚くべきことです。
上記の表で計算された数値は、予測者がポアソン不確実性が最小限のモデルを使用して作業できる完璧な世界を前提としています。ある程度の追加の不確実性(技術的に言えば、過剰分散)が存在するより現実的なモデルの場合、状況はすぐに悪化します。
製品 真の日次販売率、偏りのない日次予測 真の販売率のMAPE MAPE受賞の毎日の天気予報 MAPE受賞予測のMAPE MAPE受賞予測の予測バイアス リンゴ 0.01 99% 1 0.3% +9,900% バナナ 0.1 90% 1 3% +900% カシューナッツ 1 25% 1 25% 0% ドラゴンフルーツ 10 73% 6 53% -40% ナス 100 49% 72 40% -28%
実際の販売率で計算された MAPE 値と MAPE 勝利予測の MAPE 値の間のギャップが大幅に拡大しました。言い換えれば、MAPE で勝った予測が他の予測よりも優れているという「証拠」は、上記よりもさらに強力であるとユーザーは考えるかもしれません。しかし、MAPE 最適予測は理想的な状況よりも大きく偏っています。ドラゴンフルーツとナスの予測不足はそれぞれ 40% と 28% に達し、結果として大量の在庫切れが発生します。以下では、不確実性が高まると「安全策を講じる必要がある」ということがなぜ意味され、また「低めの水準でプレーする必要がある」ということがなぜ意味されるのかを見ていきます。
明らかに、このような戦略を採用するスーパーマーケットは長くは生き残れないでしょう。したがって、MAPE の問題はビジネスの解釈可能性 運用上の問題
MAPEはゼロカウントイベントを検閲し、壊滅的な結果をもたらす APE を計算する際、実際の値がゼロの場合にはそれを割る必要があるため、深刻な問題が発生します。この場合、APE は未定義となり、MAPE の計算には使用されません (すべての APE の平均
MAPEは予測不足と予測超過に異なるペナルティを課し、推定値の歪みにつながる。 予測 1、観察 7: APE はおよそ 6/7 です。86%。それは多いように思えますか?もしそうなら、数字を交換し、7 を予測し、1 を観察します。APE は 6/1、600% になります。APE では、特定の要因による過大予測に対して、同じ要因による過小予測よりもはるかに重いペナルティが課せられます。予測不足の場合、最悪の APE は 100% になりますが、予測過剰の場合、APE は無制限になります。その結果、結果が確実でないときはいつでも(確実であるべきではなく、すべての優れたモデルはある意味でその不確実性を認識しています)、安全策をとることは控えめな戦略をとることです。つまり、(ほぼ)どんな犠牲を払ってでも、過大な予測は避けるべきですが、大幅な過小予測が大きな負担になることはありません。したがって、最初の表で想定した予測の不確実性が最小限であっても、MAPE 最適予測は、販売率が 1 を超える場合は予測を下回るものとなります (最後の 2 行)。さらに、トレーニング データの変動性が大きいほど、モデルの不確実性が高まり、MAPE 最適予測が下方予測される可能性が高くなります。安全策を取ることはリスクを低く抑えることであり、不確実性が高まるほど、より安全を追求することになり、MAPE 最適予測は低くなります。この過剰予測に対するヘッジにより、2 番目の表の最後の 2 行に強い偏りが生じます。この非対称性は修正された MAPE によって解決されます。たとえば、パーセンテージ誤差は、実際値のみではなく、予測値と実際値の平均に対して計算できますが、これらの修正によっても非対称性は完全には解決されず、他の問題やパラドックスが発生します。
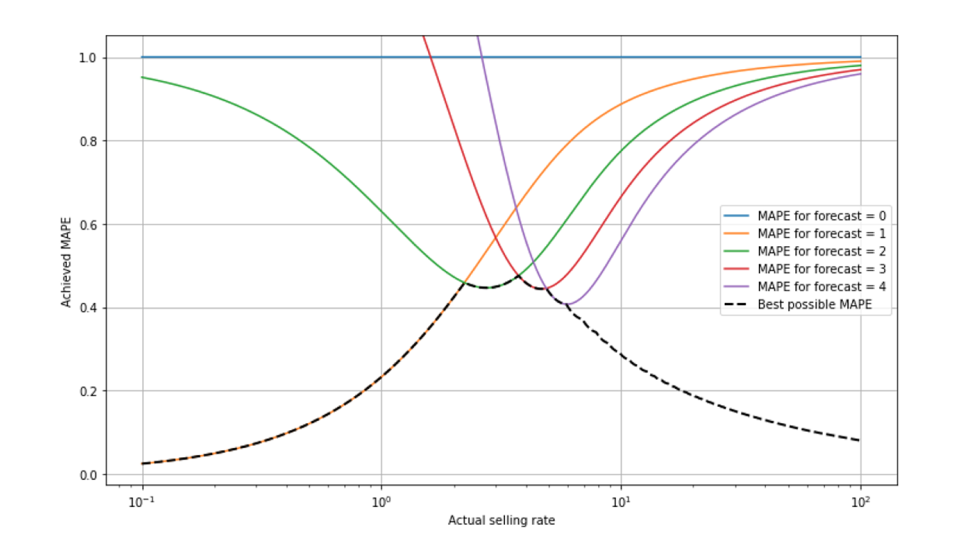
MAPEは特に複雑なスケーリング挙動を示し、予測が実際にどれほど優れているかは不明である。 確かに、解釈可能性の欠如 (50% MAPE は良いのか悪いのか?) は MAPE に固有の特徴ではありません。すべてのメトリックにはスケール依存性があり、動きの遅い企業と動きの速い企業では異なる値を想定しています。ただし、MAPE のスケーリングは、前述の 2 つの効果の組み合わせにより、特に複雑で入り組んでいます。一方では、MAPE 最適予測では 1 未満の数値が出力されることはなく、売上が 0 になる結果は削除されるだけです。一方、売却率が大きい場合、相対誤差は減少します。このグラフでは、販売率の関数として達成可能な最高の MAPE である「マウント MAPE」を示しています。
深呼吸して、あなたが見ているものを説明する機会を与えてください。x スケールは対数なので、小さな販売率をよく観察できます。スケールは 0.1 から 100 まで、非常に遅いものから速いものまであります。小売り率が約 2 を下回る場合、予測値は 1 が最適であり、左下 (黒い破線が重ねてある) から右上に向かうオレンジ色の線で示される MAPE 値が得られます。予測 2 では、売れ行きの悪い銘柄の MAPE (緑の線) が大きくなり、販売率が 0.1 の場合に 95% 近くになります。予測 0 は常に一定の MAPE 100% につながります (青い線)。0 ではない結果 (評価から除外されます) については、APE=|実際 - 0|/実際 = 100% となります。販売率が約 2.3 の場合、予測 2 が最適になるため、黒の破線 (可能な限り最高の MAPE) はオレンジ色の線から緑の線にジャンプします。さらに、最良の予測が 1 つの値から次の値にジャンプするたびに、予測が切り替わります (予測 3 と 4 はそれぞれ赤と紫で表示)。
最も優れた MAPE は、売れ行きが非常に遅い商品 (左) になるほど減少します。データから 0 件の販売イベントが削除されるため、「生き残る」イベントは主に 1 件の販売イベントとなり、商品の売れ行きが遅いほどその傾向が強まります。販売率が 0.1 の場合、1 日に 2 つのアイテムが販売される可能性はすでに非常に低く、したがって、0 以外のほとんどのケースでは予測「1」が完璧であり、達成される MAPE は非常に低くなります。つまり、データから「0」が削除され、アイテムが遅いことがわかっている場合、発生する販売数としては「1」がかなり安全な賭けになります。1 ~ 5 程度の中程度の値の場合、可能な限り最良の MAPE の「ターンテイキング」が見られます。10 以上の大きな予測の場合 (グラフの右側)、達成可能な MAPE は再び減少します。つまり、大きなレートの限界ではポアソン分布が比較的狭くなります (以前のブログ投稿「Forecasting Few is Different 1 & 2」を参照してください)。
「MAPE山」の形を一生懸命説明しました!2 つの段落で 300 語以上を費やしましたが、完全に成功していないのではないかと心配しています。予測される販売率の文脈で、将来 MAPE を直感的に判断できるような理解が得られましたか?そうならないと感じても心配しないでください。この複雑さは、専門家の間でも MAPE 値の直感的な正しい判断が広く普及する可能性は低いという、もう一つの控えめな議論です。
MAPE最適予測はビジネスとは無関係であり、潜在的な予測価値を危険にさらす。 MAPE で勝利する予測は、多くのアプリケーションで望まれるような公平な予測ではありません。しかし、「MAPE 向けに最適化する」とはどういう意味でしょうか?数学的には、MAPE を最小化する値は、統計学者向けではないブログ記事に書き留めることさえできない、扱いにくい表現を最小化します。知っておくべきこと: この表現にはビジネス上意味のある解釈はありません。在庫の確保、無駄の削減、販促や値下げの計画、商品の補充、人員計画など、予測で何を達成したいとしても、アプリケーションにおける予測の誤りによるビジネスコストはMAPEに反映されません。理想的には、「予測外れ」による実際の財務コストを反映する評価指標を選択してください。抽象的な数学関数を最適化するのではなく、ビジネス価値を最大化したいと考えています。
代替案:指標をビジネスに直接反映させる 国別で強力な仮定の下で GDP を予測するような状況を除き、MAPE は予測モデルの良し悪しを示すのに適しておらず (スケーリングのため)、2 つの競合モデルから選択するための適切な意思決定要因でもありません (MAPE が勝った予測には偏りがあります)。代替案は何ですか?最適なのは、使用されるメトリックがビジネス価値を直接反映することです。平均絶対誤差 (MAE) は、在庫過剰品 1 個のコストが欠品品 1 個のコストと同じである状況を定量化します。これは強力な仮定ですが、MAPE よりも確かに現実に近いです。MAE は予測自体と同じ次元(「項目数」)を持ち、したがって規模に大きく依存します。MAE を平均売上高で割ると、相対平均絶対誤差 (RMAE) が得られますが、ポアソン分布のスケーリング特性により、これもスケールに依存しません。したがって、スケール依存性は常に明示的に対処する必要があります。
ただし、最適な MAPE 推定値に偏りがあることを単に無視することは選択肢ではありません。重要な戦略的決定は、信頼性が高く、意味があり、ビジネスに関連した予測評価にかかっています。ソフトウェアベンダー A を使用するか、ソフトウェアベンダー B を使用するか、それとも社内ソリューションを使用するか?モデル改善の取り組みではどのような品揃えに重点を置くべきでしょうか?新しいカテゴリの予測は、自動化システムを稼働させるのに「十分」なものでしょうか?予測評価では、これらの質問やその他の多くの質問に答えるために、明確で高レベルの解釈可能で、ビジネスを反映する証拠を提供する必要があります。MAPE ではその点についてはお手伝いできません。