これは、売れ行きの速い商品と売れ行きの遅い商品に関する売上予測の取り扱いに関する 2 部構成のストーリーです。 パート1はこちらをご覧ください。
売上予測はどの程度正確になるのでしょうか?
変動キャンセルのメカニズムにより、粒度の細かい低スケールの予測は、集約された粗い高スケールの予測よりも不正確で、ノイズが多く、不確実になります。つまり、1 日のプレッツェルの総数を予測するよりも、1 週間のプレッツェルの総数を予測する方が (相対的に) 正確です。
これまで、この関係について定性的に議論してきましたが、さまざまな予測販売率に対して理想的に期待できる精度のレベルについて、定量的な説明をすることはできるでしょうか?ありがたいことに、これは確かに、業界に依存しない普遍的な方法で可能です。前回のブログ投稿では、予測評価における後知恵バイアスについて、決定論的で完全に確実な予測は非現実的であると主張しました。上記のプレッツェル 5 個の予測を考えてみましょう。個々の顧客レベルでは、確定的な予測が 5 であれば、予測された日に何があろうとプレッツェルを購入する顧客が 5 人いるということになります。しかし、私たちはこの 5 人の顧客を非常によく知っていると想定するだけでなく (おそらく、プレッツェルを取るか取らないかを自発的に決めたことがない顧客よりも彼ら自身をよく知っているかもしれません)、他の顧客がプレッツェルを購入する可能性も完全に排除します。そのような程度の確実性は明らかに不可能である。ある程度の不確実性、たとえば、プレッツェルを購入する確率がそれぞれ 5/6=83.3% の顧客が 6 人いるとすると、販売されたプレッツェルの総数に関して数学者が二項分布と呼ぶものが生じます。プレッツェルを 6 個販売する確率は (5/6)^6、プレッツェルをまったく販売しない確率は (1/6)^6、1 個から 5 個販売する確率には、それぞれの二項係数が含まれます。しかし、高い確率で購入する顧客を 6 人把握するのは、依然として非現実的です。10 人の顧客がそれぞれ 50% の確率でプレッツェルを購入すると想定するだけでも困難です。限界ポアソン分布への道をたどり、潜在的顧客の数をさらに増やしながらプレッツェルを購入する確率を下げていくことができます。ポアソン限界では、顧客数と購入確率の積、つまり販売率を制御できる一方で、すべての顧客が購入する確率が極めて小さい無制限の顧客ベースを想定します。ポアソン分布は一貫してスケーリングされます。毎日の売上が平均 5 のポアソン分布に従う場合、毎週の売上は平均 35 のポアソン分布に従います。ポアソン分布は売上予測の「ゴールドスタンダード」です。特定の製品の売上に影響を与えるすべての要因がわかっていると想定していますが、個々の顧客の購買行動についてより強力な説明を行うことができる個々の顧客データにはアクセスできません。予測精度がポアソン分布から期待されるほど良好になると、通常は、可能な範囲の限界に達したことになります。
ポアソン分布は、販売率という単一のパラメータのみを取り入れます。分布幅、つまり平均値の周りの可能性のある結果の広がりは、自己一貫性を反映する関数形式によって完全に決定されます。つまり、達成可能な精度の度合いは、考慮される時間間隔内の予測販売率によってのみ決まります。1 日あたり 5 個のプレッツェルの予測販売数は、1 週間あたり 5 個のバースデーケーキの予測販売数、1 時間あたり 5 個のパンの予測販売数、または四半期あたり 5 個のウェディングケーキの予測販売数と同じ分布に従います。言い換えれば、達成可能な最良の相対誤差は、予測値自体によって完全に一意に決定されます。
超新鮮な売れ筋商品を持続的に提供できない理由
エラースケーリングに関するこの洞察を念頭に置いて、なぜ新鮮なナマコが世界中のどこでも提供されていないのかという疑問に戻りましょう。1日あたり1個のナマコの完全なポアソン予測に対する、1日あたりの販売数の予想分布を示します。

需要がまったくない日が 37 %、魚介類愛好家が生ナマコを 1 匹購入したい日が 37 %、2 匹以上の需要がある日が 26 % になるでしょう。誰も買わなかったら一日の終わりに捨てなければならないのに、ナマコを何個在庫しておけばいいのでしょうか?在庫が 1 個しかない場合、37 % の日数はそれを廃棄する必要があり、26 % の日数は、購入しようとしていたナマコが手に入らず、お客様に不満を抱いていただくことになります。在庫が 2 個ある場合、74% の日数が経過すると少なくとも 1 個を廃棄する必要があります。多くの場所でナマコが保護されていることを考えると、これはなんとももったいないことでしょう。明らかに、生ナマコのわずかな需要を満たすことを目的としたビジネス モデルは実行可能ではなく、マージンが非常に大きい場合にのみ維持できます。生ナマコを購入する人々は、ナマコが販売されていない日すべてを補助する必要があります。そして、これらの人々は、ナマコが欲しくても確実に入手できるとは限りません。マージンと処分費用に関する控えめな仮定の下では、超新鮮で売れ行きが非常に遅い商品の適切な在庫量はゼロです。
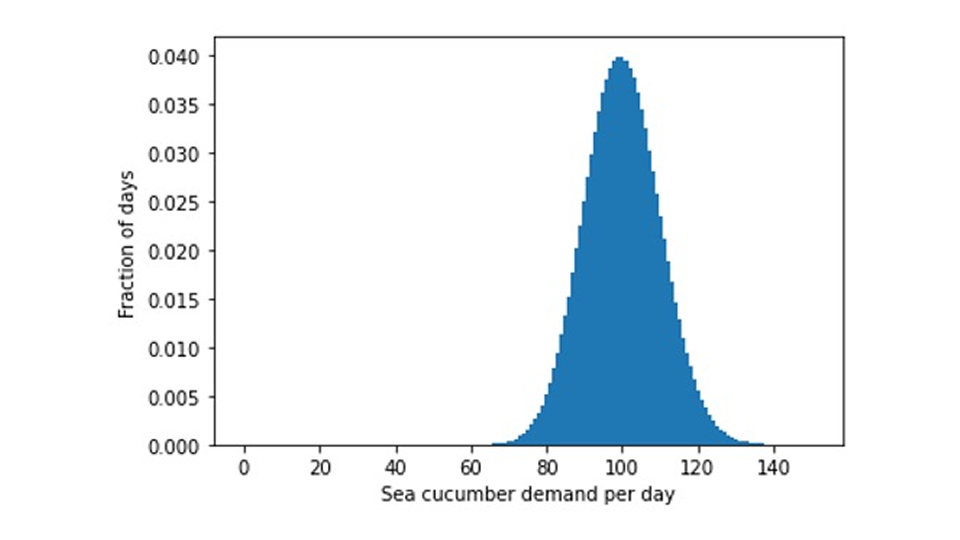
繰り返しますが、これはすべて非比例的なスケーリングによるものです。1日あたり100匹の新鮮なナマコの予測に対する販売の予想分布は、1日あたり1匹のナマコの予測の単なる膨らんだバージョンではなく、ゾウが大きなインパラのようには見えないのと同じように、異なる形をしています。
釜山でプレッツェルを、あるいは北欧でより多様なフルーツを期待している人にとっては残念なニュースです。しかし、希望はある。傷みやすい料理が流行となり、需要が一定レベルを超えると、その目新しい食べ物は新たな場所に定着する可能性がある。つまり、地球上のほぼどこでもおいしい寿司が食べられるのだ。
要約すると、予測誤差の非比例的な拡大縮小により、完璧な予測を前提としている場合でも、販売率が減少すると、製品の過剰在庫と不足在庫の発生が不比例的に増加します。その結果、特定の生鮮食品の提供は、賞味期限当たりの一定の販売率を超えた場合にのみ、維持することができます。
予測誤差の評価
なぜ国内で外国の新鮮な珍味が手に入るとは期待できないのかがわかったので、予測の質を判断する責任があるデータ サイエンティストとビジネス ユーザー向けの教訓をいくつか挙げてみましょう。予測される販売率が高い場合、実際の販売額を予測平均値に対して上下させるランダムな変動は、大幅な偏差の言い訳にはならず、そのような偏差は実際のエラーまたは予測の問題によるものとすることができます。上で説明した統計的な特異性は問題ではありません。総需要が 1,000,000 と予測され、総売上高が 800,000 だった場合、この 20% の誤差は避けられない変動によるものではなく、偏った予測によるものです。
予測数値が小さい場合、観測された偏差を悪い予測に明確に帰することはできなくなります。予測が 1 の場合、観測 0 (100% 外れ) が発生する可能性が非常に高く (確率 37%)、観測 2 (これも 100% 外れ) になる可能性も高くなります。自然のベースライン、つまり避けられないノイズが優勢になるため、予測の良し悪しを判断するのは非常に難しくなります。
それでは、観測された偏差を予測誤差によるものとみなす「売れ行きの早い銘柄」と、より寛容な「売れ行きの遅い銘柄」とに予測を分けて考えるべきでしょうか。私たちはそれをお勧めしません。中間のケース、例えば 15 という予測はどうでしょうか?「遅い」と「速い」の境界線はどこにあるのでしょうか?製品の人気が少し高まり、その境界を越えて、品質予測の判断が急に上がったらどうなるでしょうか?「速い」と「遅い」の間には、自然な境界を示さない連続的な遷移があります。これは、予測値の関数として予測の予想される相対誤差を示したこのグラフからわかります(横軸の対数目盛りと、平均ではなくポアソン分布の中央値である最適点推定値を使用して予想される誤差を計算していることに注意してください)。
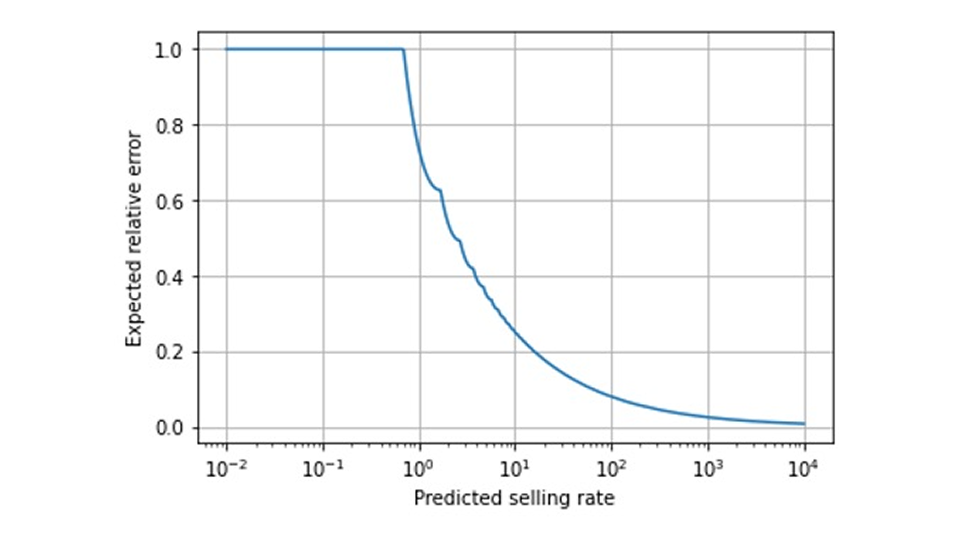
この継続的な遷移のため、予測率による層別評価を推奨します。つまり、予測を同様の予測値のビンにグループ化し、ビンごとにエラー メトリックを個別に評価します。後知恵バイアスに関する以前のブログ投稿では、このビニングを、観測された売上高ではなく予測値で行う必要がある理由について説明しています。後者の方が前者よりも自然に感じられますが。これらの各ビンについて、予測精度が理論上の期待値(上のグラフに表示)と一致しているか、それとも大幅に逸脱しているかを判断します。予測の期待値は、予測されるレートによって異なります。非常に小さい値 (0.69 未満) の場合、観測される実際の売上高のほとんどは 0 であり、必然的に「常に完全に外れて」100% の誤差が生じます。予測販売率が 10 の場合、最良の場合でも 25% という恐ろしい相対誤差を我慢しなければなりません。100=10^2 と予測すると、相対誤差は約 8% になると予想されますが、1'000=10^3 のレートでは、誤差は 2.5% に低下します。したがって、たとえば、すべての販売率にわたって 10% のエラーしきい値を求めることは逆効果です。販売が遅い企業の大多数はそのしきい値に違反し、「予測が外れている」理由を調べるためにリソースを投入しますが、しきい値に従っているために注目されない販売が速い企業については、まだいくらかの改善が可能な可能性があります。
実際には、上で描いた理想的な線からの偏差は、予測期間(明日か来年か)によって異なります。そして、業界についても(私たちは、よく知られている季節外れの食料品を予測しているのか、それともファッショナブルと無味乾燥の間の微妙な境界線上にある型破りな絶妙なドレスを予測しているのか?)。それでも、予測誤差の普遍的な非比例スケーリングを考慮することは、予測評価方法が満たすべき最も重要な側面です。
ナイーブなスケーリングの罠を避け、売れ行きの悪い商品を受け入れて戦略的に対処する
次回の休暇の必須事項リストに地元のレストラン訪問を追加するほかに、このブログ投稿からどのような結論を引き出すべきでしょうか?
評価で設定した時間的集約スケールが、ビジネス上の意思決定の時間スケールと一致していることを確認します。イチゴとナマコは 1 日しか持たないため、1 日で計画され、日レベルでの評価が適切です。今日のイチゴの需要を昨日の過剰在庫で補うことはできませんし、その逆も同様です。長持ちするアイテムの場合、ビジネス上の決定におけるエラーが実際に顕在化する規模は、決して 1 日ではありません。月曜日にシャツが購入されなかった場合は、火曜日か 2 週間後に購入される可能性があります。これは、毎月注文されるシャツの在庫にとっては重要ではありません。評価で予測数が小さい (<5) 項目が多数見つかった場合は、後者が本当に購入、補充、またはその他の決定が行われる関連項目であるかどうかを再確認してください。
製品ポートフォリオ全体にわたって、絶対的にも相対的にも、予測精度の目標を一定に設定しないでください。売れ行きの早い製品は相対誤差を簡単に低く抑えることができますが、売れ行きの遅い製品は苦労するように見えます。代わりに、予測を同様の予測値のバケットに分割し、各バケットを個別に判断します。現実的な、販売率に応じた目標を設定します。
売れ行きの悪い商品の場合、予測の確率的な性質を認識し、保存可能な商品の場合は安全在庫ヒューリスティックスを介して、またはウェディングケーキなどの注文に応じて生産する戦略を介して、大きな避けられないノイズを戦略的に考慮に入れることが必須です。
売れ行きの悪い商品では予測誤差が避けられないのがもどかしいところですが、予測技術の限界を厳密に定量的に確立し、ビジネス上の意思決定において戦略的に考慮に入れることができるようになるのは心強いことです。













